题目内容
若矩形ABCD的两条对角线的交点为M(2,0),AB边所在直线方程为x-3y-6=0,点N(-1,1)在AD边所在直线上,则矩形ABCD外接圆的标准方程为分析:由矩形的性质得到直线AD与直线AB垂直,因为两直线垂直时斜率的乘积为-1,所以由直线AB的斜率得到直线AD的斜率,又直线AD过点N,由N的坐标和求出的直线AD的斜率写出直线AD的方程,与直线AB的方程联立即可求出点A的坐标,然后利用两点间的距离公式求出|AM|的长即为矩形外接圆的半径,根据矩形的性质得到矩形外接圆的圆心即为点M,根据圆心和半径写出圆的标准方程即可.
解答:解:由题意得:AD⊥AB,又直线AB方程为x-3y-6=0,斜率为
,
所以直线AD的斜率为3,又直线AD过N(-1,1),
则直线AD的方程为y-1=3(x+1),即3x+y+2=0,
联立得:
,解得:
,
所以点A的坐标为(0,-2),又M(2,0),
则|AM|=
=2
,又矩形的外接圆的圆心为M(2,0),
∴圆M的方程为:(x-2)2+y2=8.
故答案为:(x-2)2+y2=8
| 1 |
| 3 |
所以直线AD的斜率为3,又直线AD过N(-1,1),
则直线AD的方程为y-1=3(x+1),即3x+y+2=0,
联立得:
|
|
所以点A的坐标为(0,-2),又M(2,0),
则|AM|=
| (0-2)2+(-2-0)2 |
| 2 |
∴圆M的方程为:(x-2)2+y2=8.
故答案为:(x-2)2+y2=8
点评:此题考查学生掌握矩形的性质及两直线垂直时斜率的关系,灵活运用两点间的距离公式化简求值,会根据圆心和半径写出圆的标准方程,是一道中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
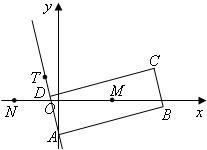 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0点T(-1,1)在AD边所在直线上.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0点T(-1,1)在AD边所在直线上. 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.