题目内容
已知两个向量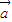 =(1+log2|x|,log2|x|),
=(1+log2|x|,log2|x|),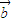 =(log2|x|,t)(x≠0).
=(log2|x|,t)(x≠0).(1)若t=1且
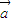
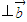 ,求实数x的值;
,求实数x的值;(2)对t∈R写出函数f(x)=
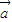
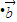 具备的性质.
具备的性质.
【答案】分析:(1)欲求实数x的值,先根据 和t=1,有(1+log2|x|,log2|x|)•(log2|x|,1)=0,再根据向量积的点坐标计算公式计算即可得出x的值.
和t=1,有(1+log2|x|,log2|x|)•(log2|x|,1)=0,再根据向量积的点坐标计算公式计算即可得出x的值.
(2)要写出函数的性质,主要看奇偶性、单调性、最值这三个方面.
解答:解:(1)由已知得log22|x|+2log2|x|=0(2分)
log2|x|=0或log2|x|=-2(4分)
解得 (6分)
(6分)
(2)f(x)=log22|x|+(1+t)log2|x|=0(8分)
具备的性质:
①偶函数;
②当 即
即 时,
时,
f(x)取得最小值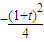 (写出值域为
(写出值域为 也可);
也可);
③单调性:在 上递减,
上递减, 上递增;
上递增;
由对称性,在[- 上递增,在
上递增,在 递减
递减
点评:本题考查平面向量综合知识,同时考查对数函数的相关知识.
 和t=1,有(1+log2|x|,log2|x|)•(log2|x|,1)=0,再根据向量积的点坐标计算公式计算即可得出x的值.
和t=1,有(1+log2|x|,log2|x|)•(log2|x|,1)=0,再根据向量积的点坐标计算公式计算即可得出x的值.(2)要写出函数的性质,主要看奇偶性、单调性、最值这三个方面.
解答:解:(1)由已知得log22|x|+2log2|x|=0(2分)
log2|x|=0或log2|x|=-2(4分)
解得
 (6分)
(6分)(2)f(x)=log22|x|+(1+t)log2|x|=0(8分)
具备的性质:
①偶函数;
②当
 即
即 时,
时,f(x)取得最小值
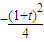 (写出值域为
(写出值域为 也可);
也可);③单调性:在
 上递减,
上递减, 上递增;
上递增;由对称性,在[-
 上递增,在
上递增,在 递减
递减点评:本题考查平面向量综合知识,同时考查对数函数的相关知识.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目