题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6.
的周长为6.
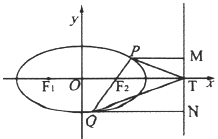
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() 与
与![]() 轴的交点为
轴的交点为![]() .若四边形
.若四边形![]() 的面积是
的面积是![]() 面积的3倍,求直线
面积的3倍,求直线![]() 斜率的取值范围.
斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)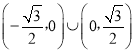 .
.
【解析】
(1)根据椭圆的离心率和焦点三角形的周长建立方程求出a,c的值即可;
(2)先设出直线PQ的方程为x=my+1,联立方程组得出根与系数关系,利用四边形PMNQ的面积是△PQT面积的3倍,得出t关于m的表达式,由t>2建立不等式,解出m的取值范围,进而根据![]() 得出k的取值范围.
得出k的取值范围.
(1)因为P是E上的点,且F1,F2为E的左、右焦点,所以|PF1|+|PF2|=2a,
又因为|F1F2|=2c,△PF1F2的周长为6,所以2a+2c=6,
又因为椭圆的离心率为![]() ,所以
,所以![]() ,解得a=2,c=1.所以
,解得a=2,c=1.所以![]() ,
,
E的方程为![]() .
.
(2)依题意,直线PQ与x轴不重合,故可设直线PQ的方程为x=my+1,
由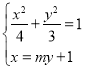 ,消去x得:(3m2+4)y2+6my-9=0,
,消去x得:(3m2+4)y2+6my-9=0,
设P(x1,y1),Q(x2,y2)则有△>0且![]() .
.
设四边形PMNQ的面积和△PQT面积的分别为S1,S2,
则S1=3S2,又因为![]() ,S2=
,S2=![]() .
.
所以![]() ,
,
即3(t-1)=2t-(x1+x2),得t=3-(x1+x2),
又x1=my1+1,x2=my2+1,于是t=3-(my1+my2+2)=1-m(y1+y2),
所以![]() ,由t>2得
,由t>2得![]() ,解得
,解得![]() ,
,
设直线PQ的斜率为k,则![]() ,所以
,所以![]() ,
,
解得![]() ,
,
所以直线PQ斜率的取值范围是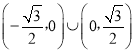 .
.

【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2014-2018年的相关数据如下表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数 | 2 | 4 | 5 | 6 | 8 |
该产品的年利润 | 30 | 40 | 60 | 50 | 70 |
年返修台数(台) | 19 | 58 | 45 | 71 | 70 |
注:![]()
(1)从该公司2014-2018年的相关数据中任意选取3年的数据,求这3年中至少有2年生产部门考核优秀的概率.
(2)利用上表中五年的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的回归直线方程是
(万台)的回归直线方程是![]() ①.现该公司计划从2019年开始转型,并决定2019年只生产该产品1万台,且预计2019年可获利32(百万元);但生产部门发现,若用预计的2019年的数据与2014-2018年中考核优秀年份的数据重新建立回归方程,只有当重新估算的
①.现该公司计划从2019年开始转型,并决定2019年只生产该产品1万台,且预计2019年可获利32(百万元);但生产部门发现,若用预计的2019年的数据与2014-2018年中考核优秀年份的数据重新建立回归方程,只有当重新估算的![]() ,
,![]() 的值(精确到0.01),相对于①中
的值(精确到0.01),相对于①中![]() ,
,![]() 的值的误差的绝对值都不超过
的值的误差的绝对值都不超过![]() 时,2019年该产品返修率才可低于千分之一.若生产部门希望2019年考核优秀,能否同意2019年只生产该产品1万台?请说明理由.
时,2019年该产品返修率才可低于千分之一.若生产部门希望2019年考核优秀,能否同意2019年只生产该产品1万台?请说明理由.
(参考公式:![]() ,
,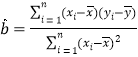
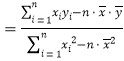 ,
,![]() ,
,![]() 相对
相对![]() 的误差为
的误差为![]() .)
.)