题目内容
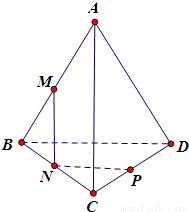
 如图,M、N、P分别为空间四边形ABCD的边AB,BC,CD上的点,且AM:MB=CN:NB=CP:PD.
如图,M、N、P分别为空间四边形ABCD的边AB,BC,CD上的点,且AM:MB=CN:NB=CP:PD.求证:(1)AC∥平面MNP,BD∥平面MNP;
(2)平面MNP与平面ACD的交线∥AC.
分析:(1)由平行线分线段成比例可知AC∥MN,由线面平行的判断可得AC∥平面MNP,同理可证BD∥平面MNP;
(2)在AD上取点Q,使CP:PD=AQ:QD,可证PQ为平面MNP与平面ACD的交线,由平行线分线段成比例易证结论.
(2)在AD上取点Q,使CP:PD=AQ:QD,可证PQ为平面MNP与平面ACD的交线,由平行线分线段成比例易证结论.
解答:解:(1)由题意AM:MB=CN:NB,由平行线分线段成比例可知:AC∥MN,
又因为MN?平面MNP,AC在平面MNP外,
由线面平行的判定定理可得:AC∥平面MNP,
同理,由CN:NB=CP:PD可得BD∥NP,
由BD在平面外,NP在平面内,故有BD∥平面MNP;
(2)在AD上取点Q,使CP:PD=AQ:QD,
由平行线分线段成比例可知:PQ∥AC,又由(1)知AC∥MN,
所以PQ∥MN,故PQ?平面MNP,又PQ?平面ACD,
所以PQ为平面MNP与平面ACD的交线,由PQ∥AC可知,
平面MNP与平面ACD的交线∥AC.
又因为MN?平面MNP,AC在平面MNP外,
由线面平行的判定定理可得:AC∥平面MNP,
同理,由CN:NB=CP:PD可得BD∥NP,
由BD在平面外,NP在平面内,故有BD∥平面MNP;
(2)在AD上取点Q,使CP:PD=AQ:QD,
由平行线分线段成比例可知:PQ∥AC,又由(1)知AC∥MN,
所以PQ∥MN,故PQ?平面MNP,又PQ?平面ACD,
所以PQ为平面MNP与平面ACD的交线,由PQ∥AC可知,
平面MNP与平面ACD的交线∥AC.
点评:本题为线面平行的证明,注意平面内外的两线是证明线面平行的关键,属中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
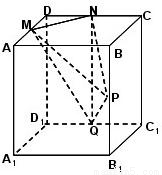
 现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.
现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.