题目内容
现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.(1)求作锯面与平面AA1C1C的交线GH,其中G、H分别在C1C、AA1上(写出作图过程即可,不必证明),并说明GH与平面ABCD的关系,然后给出证明.
(2)若Q为C1D1的中点.求点P到平面MNQ的距离.
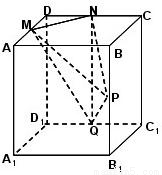
【答案】分析:(1)设MN与BC的延长线相交于点F,连PF与CC1相交于点G,设NM与BA的延长线相交于点E,连PE与AA1相交于点H,连GH,
直线GH即为平面MNP与平面AA1C1C的交线,欲证GH∥平面ABCD,根据比例关系可知GH∥EF又GH?平面ABCD,EF?平面ABCD,满足线面平行的判定定理所需条件;
(2)先证明BB1∥平面MNQ,得到点P到平面MNQ的距离等于点B到平面MNQ的距离,设BD∩MN=T,根据面面垂直的性质可知BT⊥平面MNQ,从而点P到平面MNQ的距离为BT=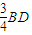 .
.
解答: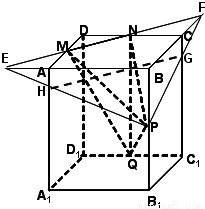 解:(1)设MN与BC的延长线相交于点F,连PF与CC1相交于点G,设NM与BA的延长线相交于点E,连PE与AA1相交于点H,连GH,
解:(1)设MN与BC的延长线相交于点F,连PF与CC1相交于点G,设NM与BA的延长线相交于点E,连PE与AA1相交于点H,连GH,
直线GH即为平面MNP与平面AA1C1C的交线,(2分)
GH∥平面ABCD,下面给出证明.(3分)
∵CG∥BP∴FG:GP=FC:CB
同理可证EH:HP=EA:AB
∵AC∥EF∴FC:CB=EA:AB
∴FG:GP=EH:HP
∴GH∥EF又GH?平面ABCD,EF?平面ABCD
∴GH∥平面ABCD(6分)
(2)∵BB1∥QN,BB1?平面MNQ,NQ⊆平面MNQ,
∴BB1∥平面MNQ,(7分)
∴点P到平面MNQ的距离等于点B到平面MNQ的距离.(9分)
设BD∩MN=T.∵平面MNQ⊥平面ABCD,∴由BT⊥MN得BT⊥平面MNQ,(10分)
∴点P到平面MNQ的距离为BT=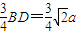 .(12分)
.(12分)
点评:本题主要考查了直线与平面平行的判定,以及点到平面的距离的求解,同时考查了作图的能力、分析问题解决问题的能力,转化与划归的思想,属于中档题.
直线GH即为平面MNP与平面AA1C1C的交线,欲证GH∥平面ABCD,根据比例关系可知GH∥EF又GH?平面ABCD,EF?平面ABCD,满足线面平行的判定定理所需条件;
(2)先证明BB1∥平面MNQ,得到点P到平面MNQ的距离等于点B到平面MNQ的距离,设BD∩MN=T,根据面面垂直的性质可知BT⊥平面MNQ,从而点P到平面MNQ的距离为BT=
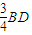 .
.解答:
 解:(1)设MN与BC的延长线相交于点F,连PF与CC1相交于点G,设NM与BA的延长线相交于点E,连PE与AA1相交于点H,连GH,
解:(1)设MN与BC的延长线相交于点F,连PF与CC1相交于点G,设NM与BA的延长线相交于点E,连PE与AA1相交于点H,连GH,直线GH即为平面MNP与平面AA1C1C的交线,(2分)
GH∥平面ABCD,下面给出证明.(3分)
∵CG∥BP∴FG:GP=FC:CB
同理可证EH:HP=EA:AB
∵AC∥EF∴FC:CB=EA:AB
∴FG:GP=EH:HP
∴GH∥EF又GH?平面ABCD,EF?平面ABCD
∴GH∥平面ABCD(6分)
(2)∵BB1∥QN,BB1?平面MNQ,NQ⊆平面MNQ,
∴BB1∥平面MNQ,(7分)
∴点P到平面MNQ的距离等于点B到平面MNQ的距离.(9分)
设BD∩MN=T.∵平面MNQ⊥平面ABCD,∴由BT⊥MN得BT⊥平面MNQ,(10分)
∴点P到平面MNQ的距离为BT=
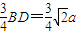 .(12分)
.(12分)点评:本题主要考查了直线与平面平行的判定,以及点到平面的距离的求解,同时考查了作图的能力、分析问题解决问题的能力,转化与划归的思想,属于中档题.

练习册系列答案
相关题目
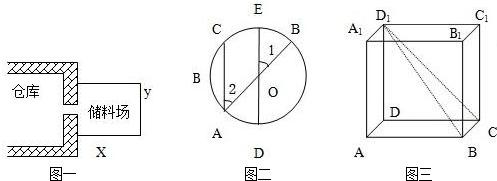
 现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.
现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.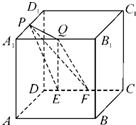 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P是A1D1的中点,Q是A1B1上的任意一点,E、F是CD上的任意两点,且EF的长为定值.现有如下结论:
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P是A1D1的中点,Q是A1B1上的任意一点,E、F是CD上的任意两点,且EF的长为定值.现有如下结论: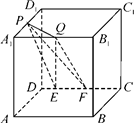 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P是A1D1的中点,Q是A1B1上任意一点,E、F是CD上任意两点,且EF的长为定值,现有如下结论:
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P是A1D1的中点,Q是A1B1上任意一点,E、F是CD上任意两点,且EF的长为定值,现有如下结论: