题目内容
已知集合A={(x,y)|x,y,2n-x-y}是三角形的三边之长,n∈N*}设an表示集合A中整点(横、纵坐标均为整数)的个数.(1)写出an的通项公式;
(2)求使得an>2 006成立的n的最小值;
(3)设列数{bn}满足:bn=n2-2an,n∈N*,其前n项和为Sn.若对任意正整数n,不等式![]() ≤m恒成立,求m的取值范围.
≤m恒成立,求m的取值范围.
解:(1) 即
即 集合A所表示的区域为下图.
集合A所表示的区域为下图.
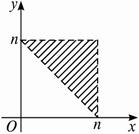 ?
?
∴an=0+1+2+…+n-2=![]() . ?
. ?
(2)∵an>2 006,∴(n-2)(n-1)>2 006×2,?
即n(n-3)>2 005×2.?
令T=x(x-3),当x>3时,该函数是增函数.经检验x=65时,T=4 030>4 010,?
x=64时,T=3 904<4 010.?
∴n≥65.∴n的最小值为65. ?
(3)bn=n2-2an=3n-2,?
bn+1-bn=3.∴数列{bn}是以1为首项,公差为3的等差数列.?
∴Sn=![]() n=
n=![]() . ?
. ?
![]() =
=![]() =Cn.?
=Cn.?
则Cn+1-Cn=-![]() ,?
,?
当n≤2时,Cn+1>Cn,即C1<C2;?
n≥3时,Cn+1<Cn,即C3>C4>C5; ?
n=2时,![]() =
=![]() ,?
,?
n=3时,![]() =3,∴M≥3.
=3,∴M≥3.
