题目内容
（2008•广州一模）根据定积分的几何意义，计算
dx=
+
+
．
| ∫ | 1 0 |
| 4-x2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
分析：由定积分的几何意义知：
dx是如图所示的阴影部分曲边梯形OABC的面积，其面积可分为扇形和三角形，分别求解即可．
| ∫ | 1 0 |
| 4-x2 |
解答：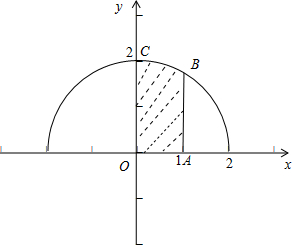
解：由定积分的几何意义知：
dx是如图所示的阴影部分曲边梯形OABC的面积，
其中B（1，
），∠BOC=30°
故
dx=S扇形BOC+S△AOB=
+
故答案为：
+
解：由定积分的几何意义知：| ∫ | 1 0 |
| 4-x2 |
其中B（1，
| 3 |
故
| ∫ | 1 0 |
| 4-x2 |
| π |
| 3 |
| ||
| 2 |
故答案为：
| π |
| 3 |
| ||
| 2 |
点评：本题考查定积分的几何意义，准确转化为图形的面积是解决问题的关键，属基础题．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
（2008•广州一模）按如图所示的程序框图运算．若输入x=8，则输出k=