题目内容
已知复数2-i是实系数一元二次方程x2+bx+c=0的一个根,
(1)求b,c值;(2)若向量
=(b,c)、
=(8,t),求实数λ和t使得
=λ
.
(1)求b,c值;(2)若向量
| m |
| n |
| m |
| n |
分析:(1)、2-i的共轭复数2+i是实系数一元二次方程x2+bx+c=0的一个根,利用一元二次方程的根与系数的关系求b,c.
(2)、根据共线向量知对应横纵坐标相等建立方程解之.
(2)、根据共线向量知对应横纵坐标相等建立方程解之.
解答:解:(1)、因为2-i是实系数一元二次方程x2+bx+c=0的一个根,
所以2+i也是实系数一元二次方程x2+bx+c=0的一个根,
所以:b=-[(2-i)+(2+i)]=-4,c=(2-i)(2+i)=5.
(2)、
=(b,c)=(-4,5),
=(8,t),
因为
=λ
,即(-4,5)=λ(8,t),
所以
,解得:λ=
,t=-10.
所以2+i也是实系数一元二次方程x2+bx+c=0的一个根,
所以:b=-[(2-i)+(2+i)]=-4,c=(2-i)(2+i)=5.
(2)、
| m |
| n |
因为
| m |
| n |
所以
|
| 1 |
| 2 |
点评:本题考查了一元二次方程的根与系数的关系,共线向量等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
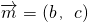 、
、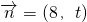 ,求实数λ和t使得
,求实数λ和t使得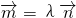 .
.