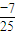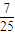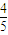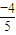题目内容
已知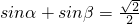 ,则cosα+cosβ的最大值是________.
,则cosα+cosβ的最大值是________.

分析:令cosα+cosβ=A与条件平方相加,利用差角的余弦公式,即可求得结论.
解答:令cosα+cosβ=A ①
又有:
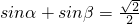 ②
②①2+②2,得(cosα+cosβ)2+(sinα+sinβ)2=A2+

∴cos2α+cos2β+2cosαcosβ+sin2α+sin2β+2sinαsinβ=A2+

∴2+2(cosαcosβ+sinαsinβ)=A2+

∴2+2cos(α-β)=A2+

∴A2=2cos(α-β)+
 ≤
≤
∴|A|≤

∴cosα+cosβ的最大值是

故答案为:

点评:本题考查三角函数的最值,考查差角的余弦公式,解题的关键是利用差角的余弦公式化简.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
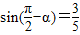 ,则cos(π-2α)=( )
,则cos(π-2α)=( )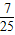
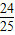
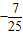
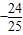
 ,则cosα+sinα等于( )
,则cosα+sinα等于( )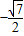
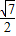

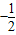
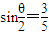 ,则cosθ的值为( )
,则cosθ的值为( )