题目内容
11.已知k4+k3+k2+k+1=0,求k2015的值.分析 利用等比数列的求和公式,可得k5=1,即可求k2015的值.
解答 解:由题意,k≠0,k≠1,
∵k4+k3+k2+k+1=0,
∴$\frac{1-{k}^{5}}{1-k}$=0,
∴k5=1,
∴k2015=(k5)403=1.
点评 本题考查等比数列的求和公式,考查学生的计算能力,比较基础.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
20.函数f(x)=$\sqrt{(x+3)^{2}+1}$+$\sqrt{(x-5)^{2}+4}$,则函数f(x)的值域是( )
| A. | [$\sqrt{73}$,+∞) | B. | (+∞,$\sqrt{73}$] | C. | [-$\sqrt{73}$,$\sqrt{73}$] | D. | [-$\sqrt{36}$,$\sqrt{36}$] |
1.设f′(x)是f(x)的导函数,如果f′(x)是二次函数,且f′(x)的图象开口向上,顶点坐标为(1,$\sqrt{3}$),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
| A. | [$\frac{π}{3}$,π) | B. | ($\frac{π}{2},\frac{2π}{3}$] | C. | [$\frac{π}{3},\frac{π}{2}$) | D. | (0,$\frac{π}{3}$] |
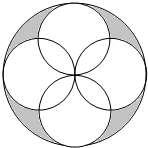 如图,用4个半径为1的小圆去覆盖一个半径为2的大圆,在大圆内随机取一点,则此点取自阴影部分的概率是$\frac{1}{2}-\frac{1}{π}$.
如图,用4个半径为1的小圆去覆盖一个半径为2的大圆,在大圆内随机取一点,则此点取自阴影部分的概率是$\frac{1}{2}-\frac{1}{π}$.