题目内容
9、已知S={β|k•360°-60°<β<k•360°+60°,k∈Z},P={α|k•180°+30°<α<k•180°+150°,k∈Z},求S∩P.
分析:讨论集合P中的k为偶数和奇数时,分别化简集合P,然后利用图象得到S与P的交集即可.
解答: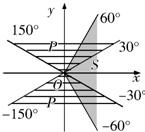 解:对于集合P,k=2n时,P={a|n•360°+30°<a<n•360°+150°,n∈Z};
解:对于集合P,k=2n时,P={a|n•360°+30°<a<n•360°+150°,n∈Z};
k=2n+1时,P={a|n•360°+210°<a<n•360°+330°,n∈Z}={a|n•360°-150°<a<n•360°-30°,n∈Z};
由图易知:S∩P={a|k•360°+30°<a<k•360°+60°,k∈Z}∪{a|k•360°-60°<a<k•360°-30°,k∈Z}
 解:对于集合P,k=2n时,P={a|n•360°+30°<a<n•360°+150°,n∈Z};
解:对于集合P,k=2n时,P={a|n•360°+30°<a<n•360°+150°,n∈Z};k=2n+1时,P={a|n•360°+210°<a<n•360°+330°,n∈Z}={a|n•360°-150°<a<n•360°-30°,n∈Z};
由图易知:S∩P={a|k•360°+30°<a<k•360°+60°,k∈Z}∪{a|k•360°-60°<a<k•360°-30°,k∈Z}
点评:本题属于以终边相同的角的范围为平台,求集合的交集的基础题,也是高考常会考的题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
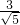 ,焦点坐标分别为F1(-2,0),F2(2,0).
,焦点坐标分别为F1(-2,0),F2(2,0). 的值;
的值;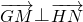 ,(s<k),分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标.
,(s<k),分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标.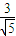 ,焦点坐标分别为F1(-2,0),F2(2,0).
,焦点坐标分别为F1(-2,0),F2(2,0).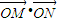 的值;
的值;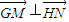 ,(s<k),分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标.
,(s<k),分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标.