题目内容
图(1)为相互成120°的三条线段,长度均为1,图(2)在第一张图的线段的前端作两条与该线段成120°的线段,长度为其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,则an=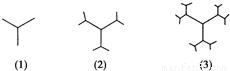
【答案】分析:先根据题意可得a1、a2、a3、a4的值,找到其中的关系,进而可得到数列的通项公式.
解答:解:依题意a1=3,a2=3+2×3× =3+3=3×2,
=3+3=3×2,
a3=3+2×3× +2×2×3×
+2×2×3× =3+3+3=3×3,
=3+3+3=3×3,
a4=3+3+3+2×12× =3+3+3+3=3×4,
=3+3+3+3=3×4,
∴an=3×n=3n.
故答案为:3n.
点评:本题主要考查数列通项公式的求法.数列的通项公式在数列学习中占据很重要的地位,要强化学习.
解答:解:依题意a1=3,a2=3+2×3×
 =3+3=3×2,
=3+3=3×2,a3=3+2×3×
 +2×2×3×
+2×2×3× =3+3+3=3×3,
=3+3+3=3×3,a4=3+3+3+2×12×
 =3+3+3+3=3×4,
=3+3+3+3=3×4,∴an=3×n=3n.
故答案为:3n.
点评:本题主要考查数列通项公式的求法.数列的通项公式在数列学习中占据很重要的地位,要强化学习.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
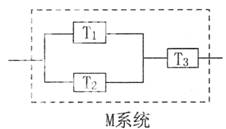 块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作.
块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作. 块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作.
块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作.