题目内容
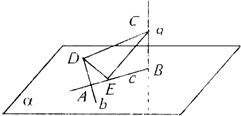（2007•青岛一模）如图所示，b、c在平面α内，a∩c=B，b∩c=A，且a⊥b，a⊥c，b⊥c，若C∈a，D∈b，E在线段AB上（C，D，E均异于A，B），则△CDE是（ ）分析：连结BD，根据直线与平面垂直的判定与性质定理得a⊥BD．下面证明∠CED＞90°．欲证∠CED＞90°，根据余弦定理，只须证明CD2-（DE2+EC2）＞0即可．在直角三角形中，利用勾股定理表示出CD2、DE2、EC2，作差后即可得出结论．
解答：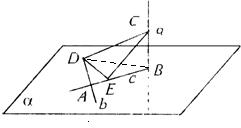
解：连结BD，
∵a⊥b，a⊥c，b、c在平面α内，
∴a⊥α，BD?α，∴a⊥BD，
在直角三角形BCD中，CD2=BD2+BC2，
同样地，在直角三角形ADE中，DE2=AD2+AE2，
在直角三角形BCE中，EC2=BC2+BE2，
∴CD2-（DE2+EC2）=BD2-AD2-AE2-BE2=AB2-（AE2+BE2）＞0，
∴∠CED＞90°，
则△CDE是钝角三角形．
故选C．
解：连结BD，∵a⊥b，a⊥c，b、c在平面α内，
∴a⊥α，BD?α，∴a⊥BD，
在直角三角形BCD中，CD2=BD2+BC2，
同样地，在直角三角形ADE中，DE2=AD2+AE2，
在直角三角形BCE中，EC2=BC2+BE2，
∴CD2-（DE2+EC2）=BD2-AD2-AE2-BE2=AB2-（AE2+BE2）＞0，
∴∠CED＞90°，
则△CDE是钝角三角形．
故选C．
点评：本小题主要考查平面的基本性质及推论、直线与平面垂直的判定与性质、解三角形等基础知识，考查运算求解能力，考查空间想象能力．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目