题目内容
下列命题中,
(1)f(x)=sinax+cosax(a≠0)既不是奇函数也不是偶函数.
(2)直线x=
是函数f(x)=sin(2x+
)的图象的一条对称轴.
(3)若α是三角形的一个内角,则f(α)=sinα+cosα有最大值
,最小值不存在.
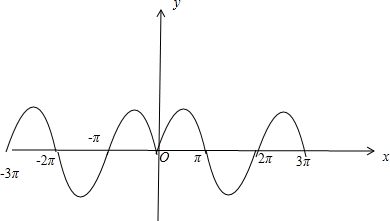
(4)函数y=sin|x|,x∈R是最小正周期为π的周期函数.
其中正确命题的序号为
(1)f(x)=sinax+cosax(a≠0)既不是奇函数也不是偶函数.
(2)直线x=
| 5π |
| 4 |
| 5π |
| 2 |
(3)若α是三角形的一个内角,则f(α)=sinα+cosα有最大值
| 2 |
(4)函数y=sin|x|,x∈R是最小正周期为π的周期函数.
其中正确命题的序号为
(1)(3)
(1)(3)
.分析:(1)f(x)=sinax+cosax=
sin(ax+
),考察f(-x)≠f(x),f(-x)≠-f(x),得出函数奇偶性;
(2)将x的值代入,看函数是否取最值即可,能取到最值就是函数的对称轴,可判断;
(3)α是三角形的内角得0<α<π,则
<α+
<
,sinα+cosα=
sin(α+
)可判断最值的取得情况;
(4)合函数y=sin|x|的图象如图可判断.
| 2 |
| π |
| 4 |
(2)将x的值代入,看函数是否取最值即可,能取到最值就是函数的对称轴,可判断;
(3)α是三角形的内角得0<α<π,则
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| 2 |
| π |
| 4 |
(4)合函数y=sin|x|的图象如图可判断.
解答:解:(1)f(x)=sinax+cosax=
sin(ax+
),则f(-x)≠f(x),f(-x)≠-f(x),函数不是奇函数也不是偶函数,故(1)正确
(2)当x=
时,y=sin(2x+
)=0,不取最值,故x=
不是对称轴,(2)不正确
(3)由α是三角形的内角得0<α<π,则
<α+
<
,sinα+cosα=
sin(α+
)有最大值
,最小值不存在,(3)正确;
(4)函数y=sin|x|得图象如图所示,由图象可知函数不是周期函数,(4)错误.
故答案为:(1)(3).
| 2 |
| π |
| 4 |
(2)当x=
| 5π |
| 4 |
| 5π |
| 2 |
| 5π |
| 4 |
(3)由α是三角形的内角得0<α<π,则
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
(4)函数y=sin|x|得图象如图所示,由图象可知函数不是周期函数,(4)错误.

故答案为:(1)(3).
点评:本题主要考察了三角函数的奇偶性的判断,三角函数的最值的求解、周期性等三角函数知识的综合的应用.

练习册系列答案
相关题目
 .
.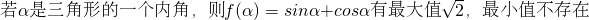 .
. .
. .
.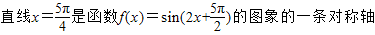 .
. .
.