题目内容
已知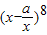 展开式中常数项为1120,其中实数a为常数.
展开式中常数项为1120,其中实数a为常数.(1)求a的值;
(2)求展开式各项系数的和.
【答案】分析:(1)二项展开式的通项为: ,要求常数项,只要令8-2r=0可求r,代入可求a
,要求常数项,只要令8-2r=0可求r,代入可求a
(2)利用赋值法,令x=1代入已知式子可求各项系数之和
解答:解:(1)二项展开式的通项为: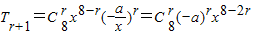
设8-2r=0则r=4.
故常数项为C84(-a)4=1120
解得a=±2
(2)当a=2时,令x=1可得展开式系数和为1
当a=-2时,令x=1展开式系数和为38.
点评:本题主要考查了利用二项展开式的通项求解展开式的指定的项,及利用赋值法求解二项展开式的各项系数之和,这是二项式定理的最常见的考试类型.
 ,要求常数项,只要令8-2r=0可求r,代入可求a
,要求常数项,只要令8-2r=0可求r,代入可求a(2)利用赋值法,令x=1代入已知式子可求各项系数之和
解答:解:(1)二项展开式的通项为:
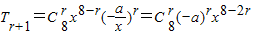
设8-2r=0则r=4.
故常数项为C84(-a)4=1120
解得a=±2
(2)当a=2时,令x=1可得展开式系数和为1
当a=-2时,令x=1展开式系数和为38.
点评:本题主要考查了利用二项展开式的通项求解展开式的指定的项,及利用赋值法求解二项展开式的各项系数之和,这是二项式定理的最常见的考试类型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是( )
展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是( ) 展开式中常数项为1120,其中实数
展开式中常数项为1120,其中实数 为常数。
为常数。 展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是
展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是 B.1或
B.1或 C.
C. 展开式中常数项为1120,其中实数
展开式中常数项为1120,其中实数 为常数。
为常数。