题目内容
已知一扇形的周长为c(c>0),当扇形的弧长为何值时,它有最大面积?并求出面积的最大值.(扇形面积S= Rl,其中R为扇形半径,l为弧长)
Rl,其中R为扇形半径,l为弧长)
当扇形的弧长为 时,扇形有最大面积,扇形面积的最大值是
时,扇形有最大面积,扇形面积的最大值是 . 12分
. 12分
解析试题分析:设扇形的半径为R,弧长为l,面积为S
∵c=2R+l,∴R= (l<c). 3分
(l<c). 3分
则S= Rl=
Rl= ×
× ·l=
·l= (cl-l2) 5分
(cl-l2) 5分
=- (l2-cl)=-
(l2-cl)=- (l-
(l- )2+
)2+ . 7分
. 7分
∴当l= 时,Smax=
时,Smax= . 10分
. 10分
答:当扇形的弧长为 时,扇形有最大面积,扇形面积的最大值是
时,扇形有最大面积,扇形面积的最大值是 . 12分
. 12分
考点:本题考查了函数的实际运用
点评:解答这类问题的关键是确切建立相关函数解析式,然后应用函数、方程和不等式的有关知识加以综合解答

练习册系列答案
相关题目
 的值
的值
 上的函数
上的函数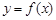 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图所示.
,其图象如图所示.
 的表达式;
的表达式;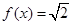 的解;
的解; 的值,使得
的值,使得
 上恒成立;若存在,求出
上恒成立;若存在,求出 ,求:
,求: 的最小正周期;
的最小正周期; 上的最大值和最小值及取得最值时
上的最大值和最小值及取得最值时 的值。
的值。 ×
× ,其中向量
,其中向量 sin2x+m).
sin2x+m). ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围. 若角
若角
 的图象按向量
的图象按向量 平移后,得到一个函数g(x)的图象,求g(x)的解析式.
平移后,得到一个函数g(x)的图象,求g(x)的解析式. 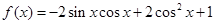
 在(0,
在(0,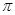 )内有两个零点
)内有两个零点 ,求
,求 的值;
的值; 的图像向左移动
的图像向左移动
 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于 轴对称,求
轴对称,求 ;
; ,
, .
. 的值;
的值; 的值域.
的值域.