题目内容
已知数列 是各项均不为
是各项均不为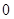 的等差数列,
的等差数列,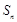 为其前
为其前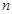 项和,且满足
项和,且满足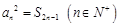 .若不等式
.若不等式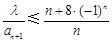 对任意的
对任意的 恒成立,则实数
恒成立,则实数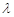 的最大值为 .
的最大值为 .
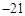
解析试题分析:由题意 ,则
,则 ,不等式
,不等式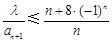 为
为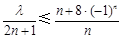 ,即
,即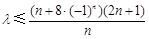 ,当
,当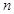 为偶数时,
为偶数时,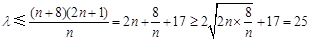 (当且仅当
(当且仅当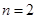 时取等号),当
时取等号),当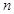 为奇数时,
为奇数时, ,函数
,函数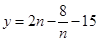 是增函数,因此
是增函数,因此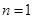 时,其取得最小值为
时,其取得最小值为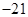 ,即
,即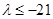 ,综上
,综上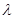 的取值范围是
的取值范围是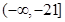 ,所以
,所以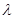 的最大值为
的最大值为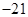 .
.
考点:数列的通项公式,数列与不等式恒成立的综合问题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
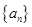 为等差数列,
为等差数列,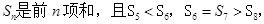 则下列结论错误的是( )
则下列结论错误的是( )
A.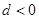 | B.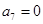 |
C.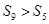 | D.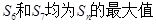 |
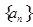 是首项为
是首项为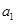 ,公差为
,公差为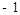 的等差数列,
的等差数列,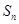 为其前
为其前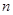 项和.若
项和.若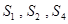 成等比数列,则
成等比数列,则 的公差
的公差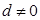 ,且
,且 成等比数列,则
成等比数列,则 的值是_______.
的值是_______.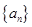 是等差数列,
是等差数列,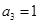 ,
,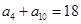 ,则首项
,则首项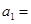 .
. 的前n项和为
的前n项和为 ,若
,若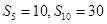 ,则
,则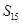 =__________。
=__________。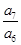 <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________.
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________.