题目内容
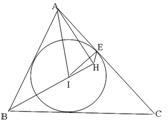
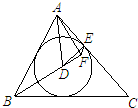 如图,锐角△ABC的内心为D,过点A作直线BD的垂线,垂足为F,点E为内切圆D与边AC的切点.若∠C=50°,求∠DEF的度数.
如图,锐角△ABC的内心为D,过点A作直线BD的垂线,垂足为F,点E为内切圆D与边AC的切点.若∠C=50°,求∠DEF的度数.分析:根据切线的性质,结合题意证出∠AED=∠AFD=90°,因此A、D、F、E四点共圆,得到∠DEF=∠DAF.由点D是△ABC的内心,可得∠DAB=
∠BAC且∠DBA=
∠ABC,结合三角形内角和定理证出∠DAB+∠DBA=
(180°-∠C)=65°,进而得到∠ADF=65°.最后在Rt△ADF中算出∠DAF=90°-∠ADF=25°,可得∠DEF=25°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵⊙D切AC于点E,∴DE⊥AC,得∠AED=90°,
又∵AF⊥DF,可得∠AFD=90°,
∴∠AED=∠AFD=90°,
因此,A、D、F、E四点共圆,在此圆中∠DEF与∠DAF对同弧,
∴∠DEF=∠DAF.
∵锐角△ABC的内心为D,
∴AD、BD分别是∠BAC、∠ABC的平分线,可得∠DAB=
∠BAC,∠DBA=
∠ABC,
因此,∠DAB+∠DBA=
(∠BAC+∠ABC)=
(180°-∠C)=
(180°-50°)=65°.
∵∠ADF为△ABD的外角,∴∠ADF=∠DAB+∠DBA=65°,
Rt△ADF中,∠DAF=90°-∠ADF=25°,可得∠DEF=∠DAF=25°.
又∵AF⊥DF,可得∠AFD=90°,
∴∠AED=∠AFD=90°,
因此,A、D、F、E四点共圆,在此圆中∠DEF与∠DAF对同弧,
∴∠DEF=∠DAF.
∵锐角△ABC的内心为D,
∴AD、BD分别是∠BAC、∠ABC的平分线,可得∠DAB=
| 1 |
| 2 |
| 1 |
| 2 |
因此,∠DAB+∠DBA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADF为△ABD的外角,∴∠ADF=∠DAB+∠DBA=65°,
Rt△ADF中,∠DAF=90°-∠ADF=25°,可得∠DEF=∠DAF=25°.
点评:本题给出△ABC的内切圆,求∠DEF的度数.着重考查了三角形内角和定理、切线的性质定理、四点共圆的判定和三角形的内切圆的性质等知识,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
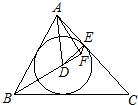 选修4-1:几何证明选讲
选修4-1:几何证明选讲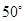 ,求∠IEH的度数.
,求∠IEH的度数.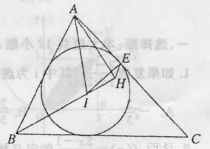
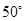 ,求∠IEH的度数.
,求∠IEH的度数.