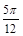题目内容
已知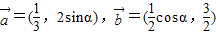 ,且
,且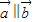 ,则锐角α的值为( )
,则锐角α的值为( )A.
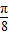
B.
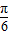
C.
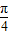
D.
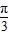
【答案】分析:利用两个向量共线的性质x1y2-x2y1=0可解得sin2α=1,从而求得锐角α的值.
解答:解:∵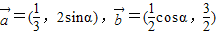 ,且
,且 ,
,
∴ =0,∴sin2α=1.
=0,∴sin2α=1.
又α为锐角,∴α= .
.
故选C.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,当两个向量共线时,有 x1y2-x2y1=0.
解答:解:∵
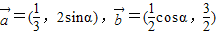 ,且
,且 ,
,∴
 =0,∴sin2α=1.
=0,∴sin2α=1.又α为锐角,∴α=
 .
.故选C.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,当两个向量共线时,有 x1y2-x2y1=0.

练习册系列答案
相关题目
已知
,
为互相垂直的单位向量,
=
-2
,
=
+λ
,且
与
的夹角为锐角,则实数λ的取值范围是( )
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
A、(-∞,
| ||||
B、(-2,
| ||||
C、(-∞,-2)∪(-2,
| ||||
D、(
|
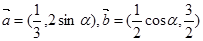 ,且
,且 ,则锐角
,则锐角 的值( )
的值( ) B.
B. C.
C.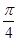 D.
D.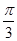
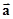 =
=
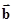 =
= ,且
,且 ,则锐角
,则锐角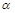 的大小为 ( )
的大小为 ( ) B.
B.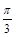 C.
C.  D.
D.