题目内容
已知函数 ,则它是( )
,则它是( )A.奇函数
B.偶函数
C.既奇又偶函数
D.非奇非偶函数
【答案】分析:首先确定函数的定义域,-2≤x≤2,且x≠0,关于原点对称,再判断f(x)与f(-x)的关系,确定函数的奇偶性.
解答:解:函数f(x)满足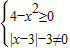 ,解得-2≤x≤2,且x≠0,定义域关于原点对称.
,解得-2≤x≤2,且x≠0,定义域关于原点对称.
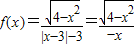 ,f(x)=-f(-x),所以函数f(x)为奇函数.
,f(x)=-f(-x),所以函数f(x)为奇函数.
故选A.
点评:本题考查了函数奇偶性的判断,关键是看定义域是否关于原点对称以及f(x)与f(-x)的关系.
解答:解:函数f(x)满足
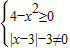 ,解得-2≤x≤2,且x≠0,定义域关于原点对称.
,解得-2≤x≤2,且x≠0,定义域关于原点对称.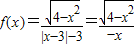 ,f(x)=-f(-x),所以函数f(x)为奇函数.
,f(x)=-f(-x),所以函数f(x)为奇函数.故选A.
点评:本题考查了函数奇偶性的判断,关键是看定义域是否关于原点对称以及f(x)与f(-x)的关系.

练习册系列答案
相关题目
 ,则它是
,则它是 ,则它的单调减区间是
,则它的单调减区间是 ,则它的单调递增区间是
,则它的单调递增区间是
 ,则它是
,则它是