题目内容
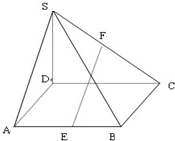 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E,F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E,F分别为AB、SC的中点,且AD=SD=2,DC=3.(1)求证:EF∥平面SAD;
(2)求异面直线AD、EF所成角的余弦值;
(3)四棱锥S-ABCD有外接球吗?若有,求出外接球的表面积;若没有,请说明理由.
分析:(1)证明EF∥平面SAD,利用线面平行的判定,证明线线平行即可,设SD的中点为G,连接GF、AG,证明EF∥AG,即可得到结论;
(2)∠GAD(或其补角)为异面直线AD,EF所成角,在Rt△GDA中,利用余弦函数可求;
(3)根据DS、DA、DC两两垂直,可知DB为四棱锥的外接球的直径,故可求四棱锥S-ABCD外接球的表面积.
(2)∠GAD(或其补角)为异面直线AD,EF所成角,在Rt△GDA中,利用余弦函数可求;
(3)根据DS、DA、DC两两垂直,可知DB为四棱锥的外接球的直径,故可求四棱锥S-ABCD外接球的表面积.
解答: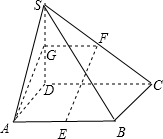 (1)证明:设SD的中点为G,连接GF、AG,则可知GF∥DC且GF=
(1)证明:设SD的中点为G,连接GF、AG,则可知GF∥DC且GF=
CD
又E为AB的中点,故AE∥DC,AE=
CD
∴GF∥AE,且GF=AE
∴四边形AEFG为平行四边形,∴EF∥AG…(2分)
又EF?平面SAD,AG?平面SAD
∴EF∥平面SAD…(4分)
(2)解:由(1)知,EF∥AG,所以∠GAD(或其补角)为异面直线AD,EF所成角….(6分)
∵SD⊥底面ABCD,∴SD⊥DA
在Rt△GDA中,AD=2,GD=1,故GA=
∴cos∠GAD=
=
,
即异面直线AD,EF所成角的余弦值为
…..(8分)
(3)解:∵DS、DA、DC两两垂直,所以可知DB为四棱锥的外接球的直径
又DB=
=
∴S=4π×(
)2=17π,即四棱锥S-ABCD外接球的表面积为17π…(12分)
 (1)证明:设SD的中点为G,连接GF、AG,则可知GF∥DC且GF=
(1)证明:设SD的中点为G,连接GF、AG,则可知GF∥DC且GF=| 1 |
| 2 |
又E为AB的中点,故AE∥DC,AE=
| 1 |
| 2 |
∴GF∥AE,且GF=AE
∴四边形AEFG为平行四边形,∴EF∥AG…(2分)
又EF?平面SAD,AG?平面SAD
∴EF∥平面SAD…(4分)
(2)解:由(1)知,EF∥AG,所以∠GAD(或其补角)为异面直线AD,EF所成角….(6分)
∵SD⊥底面ABCD,∴SD⊥DA
在Rt△GDA中,AD=2,GD=1,故GA=
| 5 |
∴cos∠GAD=
| AD |
| AG |
2
| ||
| 5 |
即异面直线AD,EF所成角的余弦值为
2
| ||
| 5 |
(3)解:∵DS、DA、DC两两垂直,所以可知DB为四棱锥的外接球的直径
又DB=
| DS2+DA2+DC2 |
| 17 |
∴S=4π×(
| ||
| 2 |
点评:本题考查线面平行,考查线线角,考查球的表面积,确定线线角,球的直径是关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
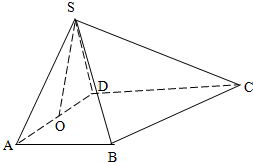 如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.