题目内容
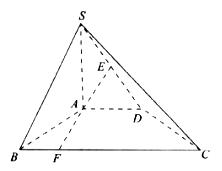
(12分)如图所示,在四棱锥S-ABCD中,侧棱SA=SB=SC=SD,低面ABCD是正方形,AC与交于点O,![]()
![]() (1)求证:AC⊥平面SBD;
(1)求证:AC⊥平面SBD;
![]() (2)当点P在线段MN上移动时,试判断EP与AC的位置关系,并证明你的结论。
(2)当点P在线段MN上移动时,试判断EP与AC的位置关系,并证明你的结论。

![]()
解析:(1)![]() 低面ABCD是正方形,O为中心,
低面ABCD是正方形,O为中心,![]() AC⊥BD
AC⊥BD
又SA=SC,![]() AC⊥SO,又SO
AC⊥SO,又SO![]() BD=0,
BD=0,![]() AC⊥平面SBD-----------------(6分)
AC⊥平面SBD-----------------(6分)
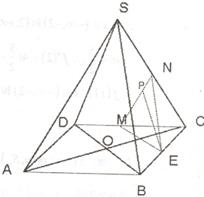
(2)连接![]()
![]()
![]()
又由(1)知,AC⊥BD
且AC⊥平面SBD,
所以,AC⊥SB---------------(8分)
![]() ⊥
⊥![]()
![]() ⊥
⊥![]() ,且EM
,且EM![]() NE=E
NE=E
![]() ⊥平面EMN-------------(10分)
⊥平面EMN-------------(10分)

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
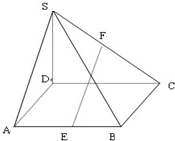 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E,F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E,F分别为AB、SC的中点,且AD=SD=2,DC=3. 如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.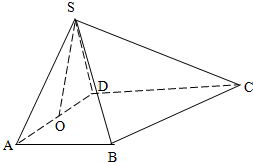 如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.