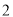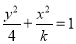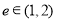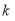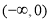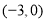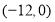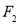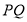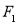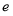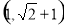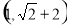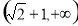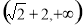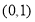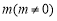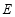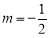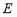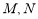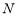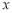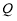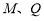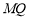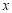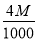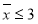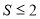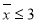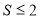题目内容
已知命题p：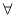
x∈[1,2]，x2-a≥0，命题q：
x0∈R，x＋2ax0＋2-a＝0，若“p且q”为真命题，求实数a的取值范围．
a＝1或a≤－2
【解析】
试题分析：求出命题p为真命题的a的范围，再通过分类讨论求出q为真命题的a的范围，“命题p∧q”为真命题，即命题q 命题p都是真命题，写出a的范围．.
试题解析：由“p且q”为真命题，则p，q都是真命题．
p：x2≥a在[1,2]上恒成立，只需a≤(x2)min＝1，
所以命题p：a≤1； 4分
q：设f(x)＝x2＋2ax＋2－a，存在x0∈R使f(x0)＝0，
只需
＝4a2－4(2－a)≥0，
即a2＋a－2≥0⇒a≥1或a≤－2，
所以命题q：a≥1或a≤－2. 8分
由
得a＝1或a≤－2
故实数a的取值范围是a＝1或a≤－2. 12分.
考点：命题的真假判断与应用．
练习册系列答案
相关题目
