题目内容
已知ai>0(i=1,2,…,n),考查
①a1•
≥1;
②(a1+a2)(
+
)≥4;
③(a1+a2+a3)(
+
+
)≥9.
归纳出对a1,a2,…,an都成立的类似不等式,并用数学归纳法加以证明.
①a1•
| 1 |
| a1 |
②(a1+a2)(
| 1 |
| a1 |
| 1 |
| a2 |
③(a1+a2+a3)(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
归纳出对a1,a2,…,an都成立的类似不等式,并用数学归纳法加以证明.
分析:依题意可归纳出:(a1+a2+…+an)(
+
+…+
)≥n2;下面用数学归纳法证明:①当n=1时易证;②假设当n=k时,不等式成立,去证明当n=k+1时,不等式也成立即可,需注意归纳假设的利用与基本不等式的应用.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
解答:结论:(a1+a2+…+an)(
+
+…+
)≥n2…(3分)
证明:①当n=1时,显然成立;…(5分)
②假设当n=k时,不等式成立,
即:(a1+a2+…+ak)(
+
+…+
)≥k2…(7分)
那么,当n=k+1时,
(a1+a2+…+ak+ak+1)(
+
+…+
+
)
=(a1+a2+…+ak)(
+
+…+
)+ak+1(
+
+…+
)+
(a1+a2+…+ak)+1
≥k2+(
+
)+(
+
)+…+(
+
)+1
≥k2+2k+1
=(k+1)2
即n=k+1时,不等式也成立.…(14分)
由①②知,不等式对任意正整数n成立.…(15分)
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
证明:①当n=1时,显然成立;…(5分)
②假设当n=k时,不等式成立,
即:(a1+a2+…+ak)(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| ak |
那么,当n=k+1时,
(a1+a2+…+ak+ak+1)(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| ak |
| 1 |
| ak+1 |
=(a1+a2+…+ak)(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| ak |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| ak |
| 1 |
| ak+1 |
≥k2+(
| ak+1 |
| a1 |
| a1 |
| ak+1 |
| ak+1 |
| a2 |
| a2 |
| ak+1 |
| ak+1 |
| ak |
| ak |
| ak+1 |
≥k2+2k+1
=(k+1)2
即n=k+1时,不等式也成立.…(14分)
由①②知,不等式对任意正整数n成立.…(15分)
点评:本题考查归纳推理与数学归纳法,着重考查归纳假设的利用与基本不等式的应用,考查推理证明的能力,属于难题.

练习册系列答案
相关题目
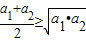 ;
;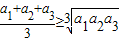 ;
;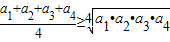 ;…;由以上不等式,我们可以推测到一个对a1,a2,…,an也成立的不等式为 .
;…;由以上不等式,我们可以推测到一个对a1,a2,…,an也成立的不等式为 .