题目内容
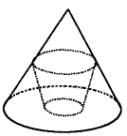
如图所示，已知圆锥的底面半径为R，高为H，在其中有一个高为x，下底面半径与上底面半径之比为λ(0<λ<1)的内接圆台．试问：当x为何值时，圆台的体积最大?并求出这个最大的体积．
答案：
解析：
解析：
设内接圆台的上底面半径为r，则下底面半径为λr．由相似三角形的性质，得r=R(1－
= = = 由 又 ∴当 故当 |
)．从而圆台的体积为
．
为定值．
时，V最大．
时，
练习册系列答案
相关题目
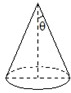已知圆锥的底面半径为5cm，侧面积为65πcm2，设圆锥的母线与高的夹角为θ（如图所示），则sinθ的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2011•延安模拟）如右图所示，已知0为矩形ABCD的边CD上一点，以直线CD为旋转轴，旋转这个矩形所得的几何体体积为1，其中以OA为母线的圆锥体积为
