题目内容
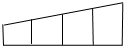如图，用6种不同的颜色给图中的4个格子涂色，每个格子涂一种颜色，要求相邻的两个格子颜色不同，则不同的涂色方法共有750
750
种（用数字作答）．分析：本题是一个分步计数问题，首先给最左边的一块涂色，有6种选择，左边第二块有5种结果，第三块有5种结果，第四块也有5种结果，相乘得到结果．
解答：解：由题意知本题是一个分步计数问题，
首先给最左边的一块涂色，有6种选择，
左边第二块有5种结果，第三块有5种结果，
第四块也有5种结果，
∴根据分步计数原理得到共有6×5×5×5=750种结果，
故答案为：750
首先给最左边的一块涂色，有6种选择，
左边第二块有5种结果，第三块有5种结果，
第四块也有5种结果，
∴根据分步计数原理得到共有6×5×5×5=750种结果，
故答案为：750
点评：本题考查分步计数问题，涂色问题是典型的排列组合问题及计数问题，并且前几年全国卷考过，本题是一个最简单的计数问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
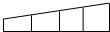15、如图，用6种不同的颜色给图中的4个格子涂色，每个格子涂一种颜色．要求最多使用3种颜色且相邻的两个格子颜色不同，则不同的涂色方法共有
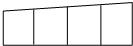16、如图，用6种不同的颜色给图中的4个格子涂色，每个格子涂一种颜色，要求相邻的两个格子颜色不同，且两端的格子的颜色也不同，则不同的涂色方法共有
种(用数字作答).