题目内容
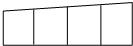 16、如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有
16、如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有630
种(用数字作答).分析:根据题意,要求相邻的两个格子颜色不同,故用到颜色最少为2种,则分用2种颜色、3种颜色、4种颜色3种情况讨论,分析计算各种情况下的情况数目,由分类计数原理计算可得答案.
解答:解:根据题意,分为三类:
第一类是只用两种颜色则为:C62A22=30种,
第二类是用三种颜色则为:C63C31C21(C21×1+1×C21)=240种,
第三类是用四种颜色则为:C64A44=360种,
由分类计数原理,共计为30+240+360=630种,
故答案为630.
第一类是只用两种颜色则为:C62A22=30种,
第二类是用三种颜色则为:C63C31C21(C21×1+1×C21)=240种,
第三类是用四种颜色则为:C64A44=360种,
由分类计数原理,共计为30+240+360=630种,
故答案为630.
点评:本题考查组合、排列的综合应用与分类计数原理的运用,注意分类时,明确分类的标准,做到不重不漏.

练习册系列答案
相关题目
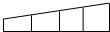 15、如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色.要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有
15、如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色.要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有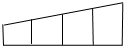 如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,则不同的涂色方法共有
如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,则不同的涂色方法共有