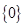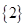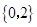题目内容
已知集合A={x|
≤0，x∈R}，B={x|x2-（1+a）x+a＞0，x∈R}，且B⊆A，求实数a的取值范围．
| x-3 |
| x-1 |
集合A={x|
≤0，x∈R}={x|（x-1）（x-3）≤0}=（1，3]
B={x|x2-（1+a）x+a＞0，x∈R}={x|（x-1）（x-a）＞0}
要使B⊆A，只要a＞3即可，故a的取值范围是（3，+∞）
| x-3 |
| x-1 |
B={x|x2-（1+a）x+a＞0，x∈R}={x|（x-1）（x-a）＞0}
要使B⊆A，只要a＞3即可，故a的取值范围是（3，+∞）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
.
;
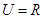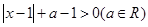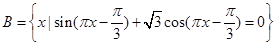，若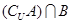
恰有3个元素，求
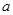的取值范围.
，
，
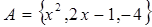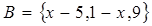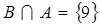，求
（ ）
，
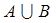
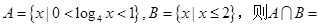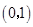
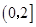
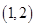
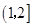
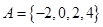，则
（ ） 
