题目内容
△ABC的两边长分别为2,3,其夹角的余弦值为,则其外接圆的半径
为( )
为( )
A. | B. | C. | D. |
C
分析:先利用余弦定理求得三角形第三边长,进而根据同角三角函数的基本关系求得第三边所对角的正弦,最后利用正弦定理求得外接圆的半径.
解答:解:由余弦定理得:三角形第三边长为
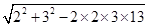 =3,
=3,
且第三边所对角的正弦值为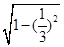 =
=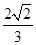 ,
,
所以由正弦定理可知2R= ,求得R=
,求得R=
故选C
点评:本题主要考查了正弦定理和余弦定理的应用.作为解三角形问题常用公式如正弦定理和余弦定理公式,勾股定理,三角形面积公式等,应作为平时训练的重点.
解答:解:由余弦定理得:三角形第三边长为
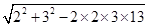 =3,
=3,且第三边所对角的正弦值为
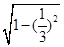 =
=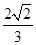 ,
,所以由正弦定理可知2R=
 ,求得R=
,求得R=
故选C
点评:本题主要考查了正弦定理和余弦定理的应用.作为解三角形问题常用公式如正弦定理和余弦定理公式,勾股定理,三角形面积公式等,应作为平时训练的重点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

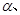
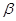 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )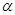 )>f(cos
)>f(cos 中,
中, ,则
,则 等于( )
等于( )





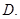

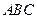 的内角
的内角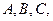 的对边分别为
的对边分别为
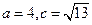 ,
,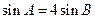 .
.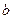 边的长;
边的长;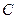 的大小。
的大小。 倍,甲船为了尽快追上乙船,则应取北偏东________(填角度)的方向前进。
倍,甲船为了尽快追上乙船,则应取北偏东________(填角度)的方向前进。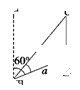
 中,如果三边
中,如果三边 依次成等比数列,那么角
依次成等比数列,那么角 的取值范围是 .
的取值范围是 . 距离为10海里的C处,此时得知,该渔船沿北偏东
距离为10海里的C处,此时得知,该渔船沿北偏东 方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.
方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.