题目内容
函数y= 的定义域是 ( ).
的定义域是 ( ).
A.[- ,-1)∪(1, ,-1)∪(1, ] ] | B.(- ,-1)∪(1, ,-1)∪(1, ) ) |
| C.[-2,-1)∪(1,2] | D.(-2,-1)∪(1,2) |
A
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数 是定义在实数集
是定义在实数集 上的以2为周期的偶函数,当
上的以2为周期的偶函数,当 时,
时, .若直线
.若直线 与函数
与函数 的图像在
的图像在 内恰有两个不同的公共点,则实数
内恰有两个不同的公共点,则实数 的值是( )
的值是( )
A. 或 或 ; ; | B.0; | C.0或 ; ; | D.0或 . . |
如图,点 从点
从点 出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周,
出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点P走过的路程
与点P走过的路程 的函数关系分别记为,定义函数
的函数关系分别记为,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
① .
.
②函数 的图象关于直线
的图象关于直线 对称.
对称.
③函数 值域为
值域为 .
.
④函数 增区间为
增区间为 .
.
| A.1 | B.2 | C.3 | D.4 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A.(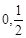 ) ) | B.( ) ) | C.( ) ) | D.( ) ) |
在区间 上不是增函数的是( )
上不是增函数的是( )
A. | B. | C. | D.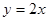 |
定义在R上的奇函数f(x),当x≥0时,f(x)= 则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ).
则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ).
| A.1-2a | B.2a-1 |
| C.1-2-a | D.2-a-1 |
若奇函数f(x)在(0,+∞)上的解析式是f(x)=x(1-x),则在(-∞,0)上,f(x)的解析式是( ).
| A.f(x)=-x(1-x) | B.f(x)=x(1+x) |
| C.f(x)=-x(1+x) | D.f(x)=x(1-x) |
 的正方体
的正方体 的对角线
的对角线 上任取一点
上任取一点 ,以
,以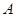 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数
 的图象大致是( ).
的图象大致是( ).