题目内容
已知角α的终边经过点P(3m-9,m+2),(1)若m=2,求5sinα+3tanα的值;
(2)若cosα≤0且sinα>0,求实数m的取值范围.
【答案】分析:(1)m=2,可求得P点坐标,利用角的正弦与正切的定义即可求得sinα,tanα的值,从而可求得5sinα+3tanα;
(2)由题意可得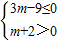 ,从而可求得实数m的取值范围.
,从而可求得实数m的取值范围.
解答:解:(1)∵m=2,
∴P(-3,4),
∴x=-3,y=4,r=5,
∴sinα=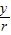 =
= ,tanα=
,tanα=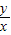 =-
=- ,
,
∴5sinα+3tanα=5× +3×(-
+3×(- )=0.
)=0.
(2)∵cosα≤0且sinα>0,
∴ ≤0且
≤0且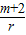 >0.
>0.
∴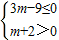
∴-2<m≤3.
∴实数m的取值范围为:-2<m≤3.
点评:本题考查任意角的三角函数的定义及由三角函数值的符号确定参数范围,掌握任意角的三角函数的定义是关键,属于基础题.
(2)由题意可得
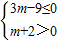 ,从而可求得实数m的取值范围.
,从而可求得实数m的取值范围.解答:解:(1)∵m=2,
∴P(-3,4),
∴x=-3,y=4,r=5,
∴sinα=
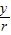 =
= ,tanα=
,tanα=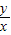 =-
=- ,
,∴5sinα+3tanα=5×
 +3×(-
+3×(- )=0.
)=0.(2)∵cosα≤0且sinα>0,
∴
 ≤0且
≤0且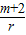 >0.
>0.∴
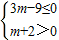
∴-2<m≤3.
∴实数m的取值范围为:-2<m≤3.
点评:本题考查任意角的三角函数的定义及由三角函数值的符号确定参数范围,掌握任意角的三角函数的定义是关键,属于基础题.

练习册系列答案
相关题目
 ,则
,则 的值等于( )
的值等于( ) B.
B. C.
C. D.
D.