题目内容
若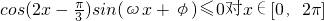 恒成立,其中ω>0,φ∈[-π,π),则ω•φ=
恒成立,其中ω>0,φ∈[-π,π),则ω•φ=
- A.
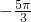
- B.

- C.

- D.

A
分析:先确定cos(2x- )≤0的x的范围,再利用
)≤0的x的范围,再利用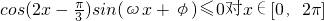 恒成立,可得sin(ωx+φ)≥0,利用ω>0,φ∈[-π,π),即可求得结论.
恒成立,可得sin(ωx+φ)≥0,利用ω>0,φ∈[-π,π),即可求得结论.
解答:∵x∈[0,2π]
∴2x- ∈[-
∈[- ,
, ]
]
∴2x- ∈[
∈[ ],即x∈[
],即x∈[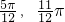 ]时,cos(2x-
]时,cos(2x- )≤0
)≤0
∴ωx+φ∈[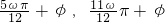 ]
]
又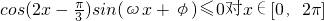 恒成立
恒成立
∴sin(ωx+φ)≥0,
∵ω>0,φ∈[-π,π),
∴
∴ω=2,φ=-
∴ω•φ=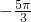
故选A.
点评:本题考查恒成立问题,考查解析式的确定,考查学生分析解决问题的能力,属于中档题.
分析:先确定cos(2x-
 )≤0的x的范围,再利用
)≤0的x的范围,再利用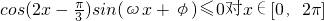 恒成立,可得sin(ωx+φ)≥0,利用ω>0,φ∈[-π,π),即可求得结论.
恒成立,可得sin(ωx+φ)≥0,利用ω>0,φ∈[-π,π),即可求得结论.解答:∵x∈[0,2π]
∴2x-
 ∈[-
∈[- ,
, ]
]∴2x-
 ∈[
∈[ ],即x∈[
],即x∈[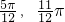 ]时,cos(2x-
]时,cos(2x- )≤0
)≤0∴ωx+φ∈[
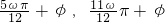 ]
]又
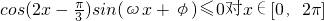 恒成立
恒成立∴sin(ωx+φ)≥0,
∵ω>0,φ∈[-π,π),
∴

∴ω=2,φ=-

∴ω•φ=
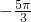
故选A.
点评:本题考查恒成立问题,考查解析式的确定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 恒成立,其中ω>0,φ∈[-π,π),则ω•φ=( )
恒成立,其中ω>0,φ∈[-π,π),则ω•φ=( )



 恒成立,其中ω>0,φ∈[-π,π),则ω•φ=( )
恒成立,其中ω>0,φ∈[-π,π),则ω•φ=( )


