题目内容
设定义域在[x1,x2]的函数y=f(x)的图象为C,C的端点分别为A、B,M是C上的任一点,向量| OA |
| OB |
| OM |
| ON |
| OA |
| OB |
| MN |
(1)证明:0≤λ≤1(2);
(3)请你给出一个标准K的范围,使得[0,1]上的函数y=x2(4)与y=x3(5)中有且只有一个可在标准K下线性近似.
分析:(1)据区间的左端点小于等于右端点,列出x1≤x≤x2,将x的值代入解不等式.
(2)对于y=x2与y=x3分别求出M,N两点的距离的最大值,利用题目中的定义求出K的范围.
(2)对于y=x2与y=x3分别求出M,N两点的距离的最大值,利用题目中的定义求出K的范围.
解答:解:(1)由题意,x1≤x≤x2,即x1≤λx1+(1-λ)x2≤x2,∴x1-x2≤λ(x1-x2)≤0.
∵x1-x2<0,∴0≤λ≤1.
(2)由
=λ
+(1-λ)
所以B、N、A三点在一条直线上.
又由(1)的结论,N在线段AB上,且与点M的横坐标相同.
对于[0,1]上的函数y=x2,A(0,0),B(1,1),
则有||
||=x-x2=
-(x-
)2,故|
|∈[0,
].
对于[0,1]上的函数y=x3,则有=x-x3=g(x).
在(0,1)上,g′(x)=1-3 x2,
可知在(0,1)上y=g(x)只有一个极大值点x=
,
所以函数y=g(x)在(0,
)上是增函数;在(
,1)上是减函数.
又g(
)=
,故[0,|
|∈[0,
]].
经过比较,
<
,所以取k[
,
),则有函数y=x2在[0,1]上可在标准k下线性近似,函数y=x3在[0,1]上不可在标准k下线性近似.
∵x1-x2<0,∴0≤λ≤1.
(2)由
| ON |
| OA |
| OB |
所以B、N、A三点在一条直线上.
又由(1)的结论,N在线段AB上,且与点M的横坐标相同.
对于[0,1]上的函数y=x2,A(0,0),B(1,1),
则有||
| MN |
| 1 |
| 4 |
| 1 |
| 2 |
| MN |
| 1 |
| 4 |
对于[0,1]上的函数y=x3,则有=x-x3=g(x).
在(0,1)上,g′(x)=1-3 x2,
可知在(0,1)上y=g(x)只有一个极大值点x=
| ||
| 3 |
所以函数y=g(x)在(0,
| ||
| 3 |
| ||
| 3 |
又g(
| ||
| 3 |
2
| ||
| 9 |
| MN |
2
| ||
| 9 |
经过比较,
| 1 |
| 4 |
2
| ||
| 9 |
| 1 |
| 4 |
2
| ||
| 9 |
点评:本题考查解不等式的能力及求函数最值的方法,新定义题在高考中近几年常出现.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
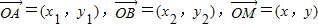 ,若x=λx1+(1-λ)x2,记向量
,若x=λx1+(1-λ)x2,记向量 ,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指
,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指 恒成立,其中K是一个正数.
恒成立,其中K是一个正数.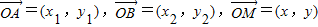 ,若x=λx1+(1-λ)x2,记向量
,若x=λx1+(1-λ)x2,记向量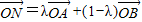 ,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指
,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指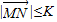 恒成立,其中K是一个正数.
恒成立,其中K是一个正数.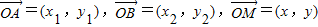 ,若x=λx1+(1-λ)x2,记向量
,若x=λx1+(1-λ)x2,记向量 ,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指
,现定义“函数y=f(x)在[x1,x2]上可在标准K下线性近似”是指 恒成立,其中K是一个正数.
恒成立,其中K是一个正数.