题目内容
已知x+y=1(x>0,y>0),求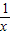 +
+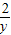 的最小值,请仔细阅读下列解法,并在填空处回答指定问题:
的最小值,请仔细阅读下列解法,并在填空处回答指定问题:解析:∵x+y=1,令x=cos2θ,y=sin2θ,
则
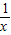 +
+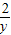 =
=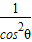 +
+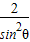 =tan2θ+2cot2θ+3≥3+2
=tan2θ+2cot2θ+3≥3+2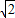 .
.①指出运用了 数学方法;
②指出θ的一个取值范围 ;
③指出x、y的取值范围 .
【答案】分析:本题考查的知识点是简单的演绎推理,根据利用基本不等式求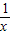 +
+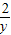 的最小值的解题过程对3个问题逐一判断即可得到答案.
的最小值的解题过程对3个问题逐一判断即可得到答案.
解答:解:由于题中:“令x=cos2θ,y=sin2θ”,是利用三角函数中的平方关系进行换元,
故①处填:换元法;
由于换元后要保证x>0,y>0,故可考虑θ的一个取值范围是锐角,
故②处填:θ∈(0,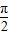 );
);
考虑到使得:“tan2θ+2cot2θ+3≥3+2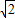 ”中等号成立,
”中等号成立,
必须满足:tanθ=2cotθ,即tanθ=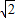 ,
,
由三角函数的同角公式得:x=2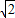 -1,y=2-
-1,y=2-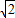 ,
,
故③处填:x=2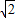 -1,y=2-
-1,y=2-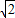 时,
时,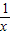 +
+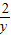 取得最小值3+2
取得最小值3+2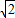 .
.
故答案为:换元法;θ∈(0,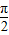 );x=2
);x=2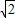 -1,y=2-
-1,y=2-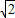 时,
时,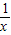 +
+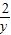 取得最小值3+2
取得最小值3+2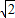 .
.
点评:演绎推理又称三段论推理,是由两个前提和一个结论组成,大前提是一般原理(规律),即抽象得出一般性、统一性的成果;小前提是指个别对象,这是从一般到个别的推理,从这个推理,然后得出结论.又称从规律到现象的推理.
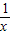 +
+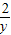 的最小值的解题过程对3个问题逐一判断即可得到答案.
的最小值的解题过程对3个问题逐一判断即可得到答案.解答:解:由于题中:“令x=cos2θ,y=sin2θ”,是利用三角函数中的平方关系进行换元,
故①处填:换元法;
由于换元后要保证x>0,y>0,故可考虑θ的一个取值范围是锐角,
故②处填:θ∈(0,
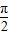 );
);考虑到使得:“tan2θ+2cot2θ+3≥3+2
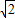 ”中等号成立,
”中等号成立,必须满足:tanθ=2cotθ,即tanθ=
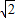 ,
,由三角函数的同角公式得:x=2
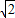 -1,y=2-
-1,y=2-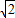 ,
,故③处填:x=2
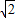 -1,y=2-
-1,y=2-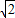 时,
时,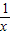 +
+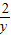 取得最小值3+2
取得最小值3+2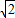 .
.故答案为:换元法;θ∈(0,
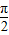 );x=2
);x=2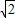 -1,y=2-
-1,y=2-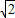 时,
时,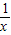 +
+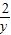 取得最小值3+2
取得最小值3+2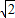 .
.点评:演绎推理又称三段论推理,是由两个前提和一个结论组成,大前提是一般原理(规律),即抽象得出一般性、统一性的成果;小前提是指个别对象,这是从一般到个别的推理,从这个推理,然后得出结论.又称从规律到现象的推理.

练习册系列答案
相关题目
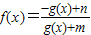 是奇函数.
是奇函数.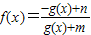 是奇函数.
是奇函数.