题目内容
若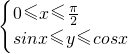 z=x+2y,则z的取值范围是________.
z=x+2y,则z的取值范围是________.

分析:作出题中不等式组表示的平面区域,得到如图所示的阴影部分.将直线l:z=x+2y进行平移并加以观察,可得当直线ly经过原点时,z达到最小值0;当直线l与余弦曲线相切于点A时,z达到最大值,用导数求切线的方法算出A的坐标并代入目标函数,即可得到z的最大值.由此即可得到实数z的取值范围.
解答:
 解:作出可行域如图所示,可得直线l:z=x+2y与y轴交于点
解:作出可行域如图所示,可得直线l:z=x+2y与y轴交于点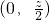 .
.观察图形,可得直线l:z=x+2y经过原点时,z达到最小值0
直线l:z=x+2y与曲线
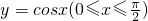 相切于点A时,z达到最大值.
相切于点A时,z达到最大值.∵由
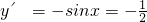 得
得 ,
,∴代入函数表达式,可得
 ,
,由此可得zmax=
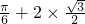 =
=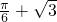 .
.综上所述,可得z的取值范围为
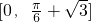 .
.故答案为:
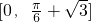
点评:本题给出约束条件,求目标函数z=x+2y的取值范围.着重考查了简单线性规划和运用导数求函数图象的切线的知识,属于中档题.

练习册系列答案
相关题目
设x,y满足约束条件
,若z=
的最小值为
,则a的值( )
|
| x+2y+3 |
| x+1 |
| 3 |
| 2 |
| A、1 | B、3 | C、4 | D、12 |
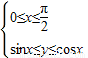 ,z=x+2y,则z的取值范围是 .
,z=x+2y,则z的取值范围是 .