题目内容
、如图:已知椭圆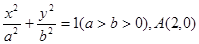 是长轴的一个端点,弦BC过椭圆的中心O,且
是长轴的一个端点,弦BC过椭圆的中心O,且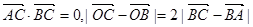 .
.

(1)求椭圆的方程;
(2)若AB上的一点F满足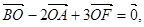 求证:CF平分∠BCA;
求证:CF平分∠BCA;
(3)对于椭圆上的两点P、Q,∠PCQ的平分线总是垂直于x轴时,是否存在实数λ,使得
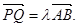
(1) ;(Ⅱ)证明见解析;(Ⅲ)存在实数λ,使得
;(Ⅱ)证明见解析;(Ⅲ)存在实数λ,使得 .
.
【解析】(I) 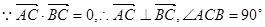
又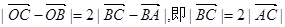 ,∴△AOC是等腰直角三角形.
,∴△AOC是等腰直角三角形.
这样可由A(2,0),得到C(1,1),根据点C在椭圆上,a=2,可求出椭圆方程.
(II)因为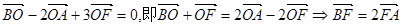 ,
,
从而可知F为有向线段BA的内分点,再借助分点坐标公式求出F的坐标.再证明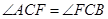 即可.
即可.
(III)对于椭圆上两点P、Q,∵∠PCQ的平分线总是垂直于x轴
∴PC与CQ所在直线关于x=1对称,kpC=k,则kcQ=-k,设C(1,1),则PC的直线方程y-1=k(x-1)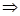 y=k(x-1)+1 ,QC的直线方y-1=-k(x-1)
y=k(x-1)+1 ,QC的直线方y-1=-k(x-1) 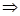 y=-k(x-1)+1,将直线PC的方程与椭圆方程联立消y得关于x的一元二次方程,可知x=1是其方程的一个根,这样可根据韦达定理可求出另一个根xp;同样的方法可求出xQ,从而可利用
y=-k(x-1)+1,将直线PC的方程与椭圆方程联立消y得关于x的一元二次方程,可知x=1是其方程的一个根,这样可根据韦达定理可求出另一个根xp;同样的方法可求出xQ,从而可利用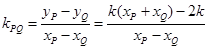 求出PQ斜率,如果与AB的斜率相等,就说明这两个向量共线,从而说明存在实数λ,使得
求出PQ斜率,如果与AB的斜率相等,就说明这两个向量共线,从而说明存在实数λ,使得 .
.
解: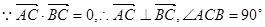
又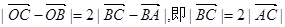
∴△AOC是等腰直角三角形. ∵A(2,0),∴C(1,1)而点C在椭圆上,
∴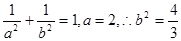 . ∴所求椭圆方程为
. ∴所求椭圆方程为
(Ⅱ)证明C(1,1),则B(-1,-1)
又
即点F分 所成的定比为2. 设
所成的定比为2. 设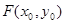
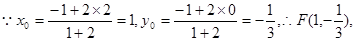
CF⊥x轴, ∴∠ACF=∠FCB=45°,即CF平分∠BCA.
(Ⅲ)对于椭圆上两点P、Q,∵∠PCQ的平分线总是垂直于x轴
∴PC与CQ所在直线关于x=1对称,kpC=k,则kcQ=-k,
设C(1,1),则PC的直线方程y-1=k(x-1)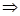 y=k(x-1)+1 ①
y=k(x-1)+1 ①
QC的直线方y-1=-k(x-1) 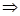 y=-k(x-1)+1 ②
y=-k(x-1)+1 ②
将①代入 得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 ③
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 ③
∵C(1,1)在椭圆上,∴x=1是方程③的一个根,
∴xp·1=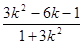 =1同理将②代入x2+3y2=4得
=1同理将②代入x2+3y2=4得
(1+3k2)x2-6k(k+1)x+3k2+6k-1=0 ④
∵C(1,1)在椭圆上, ∴x=1是方程④的一个根,
∴xQ·1= 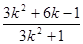
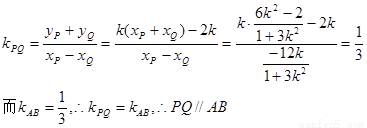
∴存在实数λ,使得 .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 的长轴为
的长轴为 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率

 是椭圆上异于
是椭圆上异于 、
、 轴,
轴, 为垂足,延长
为垂足,延长 到点
到点 使得
使得 ,连接
,连接 并延长交直线
并延长交直线 ,
, 为
为 的中点.试判断直线
的中点.试判断直线 与以
与以 的位置关系.
的位置关系.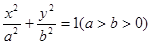 的长轴为
的长轴为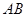 ,过点
,过点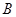 的直线
的直线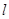 与
与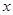 轴垂直,直线
轴垂直,直线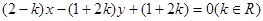 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率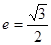
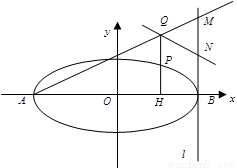
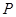 是椭圆上异于
是椭圆上异于 、
、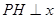 轴,
轴,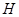 为垂足,延长
为垂足,延长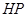 到点
到点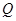 使得
使得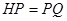 ,连接
,连接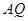 并延长交直线
并延长交直线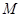 ,
,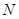 为
为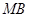 的中点.试判断直线
的中点.试判断直线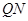 与以
与以 的位置关系.
的位置关系. 的长轴为
的长轴为 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
 是椭圆上异于
是椭圆上异于 、
、 轴,
轴, 为垂足,延长
为垂足,延长 到点
到点 使得
使得 ,连接
,连接 并延长交直线
并延长交直线 ,
, 为
为 的中点.试判断直线
的中点.试判断直线 与以
与以 的位置关系.
的位置关系.

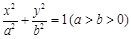 的长轴为
的长轴为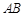 ,过点
,过点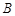 的直线
的直线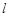 与
与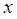 轴垂直.直线
轴垂直.直线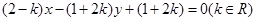 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率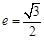 。
。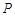 是椭圆上异于
是椭圆上异于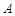 、
、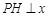 轴,
轴,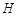 为垂足,延长
为垂足,延长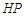 到点
到点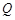 使得
使得 ,连结
,连结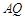 延长交直线
延长交直线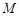 ,
, 为
为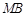 的中点.试判断直线
的中点.试判断直线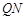 与以
与以 的位置关系。
的位置关系。