题目内容
(本题满分12分)
如图,已知椭圆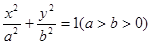 的长轴为
的长轴为 ,过点
,过点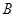 的直线
的直线 与
与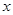 轴垂直,直线
轴垂直,直线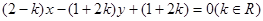 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率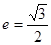

(1)求椭圆的标准方程;
(2)设 是椭圆上异于
是椭圆上异于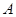 、
、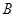 的任意一点,
的任意一点,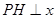 轴,
轴,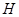 为垂足,延长
为垂足,延长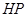 到点
到点 使得
使得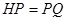 ,连接
,连接 并延长交直线
并延长交直线 于点
于点 ,
, 为
为 的中点.试判断直线
的中点.试判断直线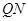 与以
与以 为直径的圆
为直径的圆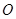 的位置关系.
的位置关系.
【答案】
(1) ;(2)直线
;(2)直线 与以
与以 为直径的圆
为直径的圆 相切。
相切。
【解析】本试题主要是考查了直线与椭圆的位置关系的运用。
(1)将已知直线方程整理得到过定点(0,1),从而得到b的值,然后结合离心率公式得到其方程。
(2)设出点P,利用PQ=PH,得到关系式,进而化简得到直线的方程,以及向量的坐标得到证明。
解:(1)将 整理得
整理得 ,解方程组
,解方程组 得直线所经过的定点为
得直线所经过的定点为 。
。
由离心率 ,得
,得 。
。 椭圆的标准方程为
椭圆的标准方程为  ……5分
……5分
(1) 设 ,则
,则 。
。 ,
,
 ,
,
 点在以
点在以 为圆心,2为半径的圆上,即
为圆心,2为半径的圆上,即 点在以
点在以 为直径的圆
为直径的圆 上。
上。
又 直线l的方程为
直线l的方程为 。令
。令 ,得
,得 。
。
又 ,
, 的中点,
的中点,
 ,
,
 直线
直线 与以
与以 为直径的圆
为直径的圆 相切……12分
相切……12分

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
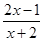 <1,xÎR }.
<1,xÎR }.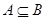 ,求实数a的取值范围.
,求实数a的取值范围.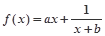 (
(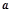 ,
,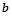 为常数),且方程
为常数),且方程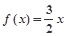 有两个实根为
有两个实根为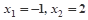 .
.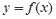 的解析式;
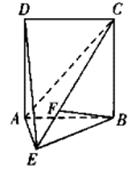
的解析式;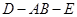 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
,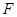 为
为 上的点,且
上的点,且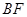 ⊥平面
⊥平面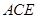
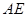 ⊥平面
⊥平面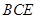
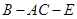 的大小;
的大小;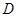 到平面
到平面