题目内容
已知函数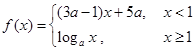 ,现给出下列命题:
,现给出下列命题:
① 当图象是一条连续不断的曲线时,则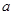 =
=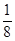 ;
;
② 当图象是一条连续不断的曲线时,能找到一个非零实数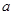 ,使
,使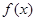 在
在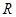 上是增函数;
上是增函数;
③ 当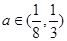 时,不等式
时,不等式 恒成立;
恒成立;
④ 函数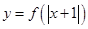 是偶函数.
是偶函数.
其中正确的命题是
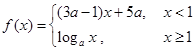 ,现给出下列命题:
,现给出下列命题:① 当图象是一条连续不断的曲线时,则
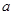 =
=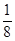 ;
;② 当图象是一条连续不断的曲线时,能找到一个非零实数
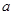 ,使
,使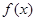 在
在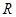 上是增函数;
上是增函数; ③ 当
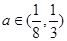 时,不等式
时,不等式 恒成立;
恒成立;④ 函数
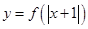 是偶函数.
是偶函数.其中正确的命题是
| A.① ④ | B.② ④ | C.① ③ | D.② ③ |
C
试题分析:∵图象是一条连续不断的曲线,当x=1时,则函数值满足
∴8a-1=0,a=
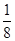 ,故①正确;
,故①正确;当图象是一条连续不断的曲线时,
a=
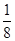 ,f (x)在R上是减函数,故②不正确;
,f (x)在R上是减函数,故②不正确;当a∈{m|
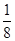 <m<
<m<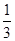 ,m∈R}时,不等式f(1+a)•f(1-a)<0恒成立,故③正确;
,m∈R}时,不等式f(1+a)•f(1-a)<0恒成立,故③正确;函数 y=f(|x+1|)是偶函数不成立.即④不正确.
故选C
点评:解决该试题的关键是对于函数连续不断的理解和运用函数的单调性得到参数a是否存在的怕你的功能,同时结合不等式来证明恒成立问题。

练习册系列答案
相关题目
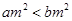 ”,则“
”,则“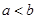 ”的逆命题是真命题
”的逆命题是真命题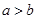 ”是“
”是“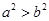 ”的充要条件;
”的充要条件;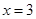 ”是“
”是“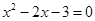 ”的必要不充分条件;
”的必要不充分条件;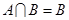 ”是“
”是“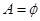 ”的必要不充分条件.
”的必要不充分条件.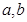 都是奇数,则
都是奇数,则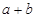 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若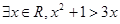 ”的否定是“
”的否定是“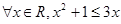 ” ;
” ;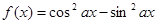 的最小正周期为
的最小正周期为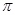 ” 是“
” 是“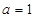 ”的必要不充分条件;
”的必要不充分条件;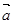 与
与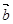 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“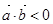 ” .
” .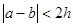 ,命题乙为:两个实数a、b满足
,命题乙为:两个实数a、b满足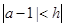 且
且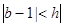 ,那么
,那么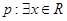 ,使
,使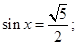 命题
命题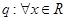 ,都有
,都有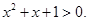 给出下列结论:① 命题“
给出下列结论:① 命题“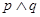 ”是真命题 ② 命题“
”是真命题 ② 命题“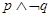 ”是假命题
”是假命题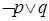 ”是真命题 ④ 命题“
”是真命题 ④ 命题“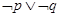 ”是假命题其中正确的是( )
”是假命题其中正确的是( )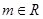 ,命题
,命题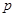 :对任意
:对任意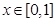 ,不等式
,不等式 恒成立;命题
恒成立;命题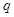 :存在
:存在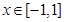 ,使得
,使得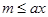 成立
成立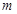 的取值范围;
的取值范围;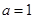 ,若
,若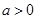 且
且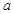 的取值范围。
的取值范围。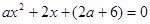 有一正一负根的充要条件是a
有一正一负根的充要条件是a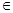 ______.
______.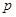 :
: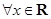 ,
,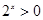 ,那么命题
,那么命题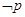 为( )
为( )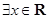 ,
,