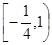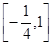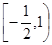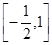题目内容
直线经过点A(2,1),B(1,m2)两点(m∈R),那么直线l的倾斜角取值范围是 ( )
A.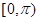 | B.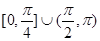 | C.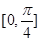 | D.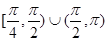 |
B
解析试题分析:设直线AB的倾斜角为θ,0≤θ<π,根据斜率的计算公式,可得AB的斜率为 K=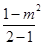 =1-m2,进而可得K的范围,由倾斜角与斜率的关系,可得tanθ≤1,进而由正切函数的图象分析可得答案。解:设直线AB的倾斜角为θ,0≤θ<π,根据斜率的计算公式,可得AB的斜率为 K=
=1-m2,进而可得K的范围,由倾斜角与斜率的关系,可得tanθ≤1,进而由正切函数的图象分析可得答案。解:设直线AB的倾斜角为θ,0≤θ<π,根据斜率的计算公式,可得AB的斜率为 K=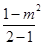 =1-m2,易得k≤1,由倾斜角与斜率的关系,可得tanθ≤1,由正切函数的图象,可得θ的范围是
=1-m2,易得k≤1,由倾斜角与斜率的关系,可得tanθ≤1,由正切函数的图象,可得θ的范围是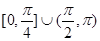 故选B.
故选B.
考点:直线的倾斜角
点评:本题考查直线的倾斜角,要求学生结合斜率的计算公式,结合斜率与倾斜角的关系,进行分析求解

练习册系列答案
相关题目
如果两条直线l1: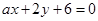 与l2:
与l2: 平行,那么
平行,那么 等于( )
等于( )
A.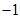 | B.2 | C.2或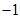 | D.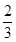 |
已知点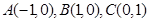 ,直线
,直线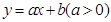 将△
将△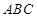 分割为面积相等的两部分,则
分割为面积相等的两部分,则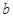 的取值范围是( )
的取值范围是( )
A.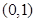 | B.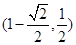 | C.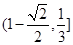 | D.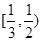 |
直线xsinα+y+2=0的倾斜角的取值范围是( ).
| A.[0,π) | B.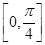 ∪ ∪ |
C.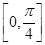 | D.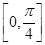 ∪ ∪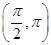 |
已知直线的倾斜角为45°,在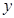 轴上的截距为2,则此直线方程为( )
轴上的截距为2,则此直线方程为( )
A.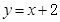 . . | B.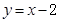 | C.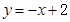 | D.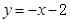 |
过点M(1,-2)的直线与x轴、y轴分别交于P、Q两点,若M恰为线段PQ的中点,则直线PQ的方程为( )
| A.2x+y=0 | B.x-2y-5=0 | C.x+2y+3=0 | D.2x-y-4=0 |
直线x+y=1和直线2mx-y=4互相垂直,则m的值是( )
A.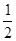 | B.4 | C.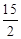 | D.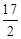 |
已知点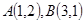 ,则线段
,则线段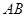 的垂直平分线的方程是( )
的垂直平分线的方程是( )
A.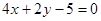 | B.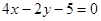 |
C. | D.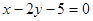 |
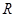 上的函数
上的函数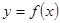 是减函数,且函数
是减函数,且函数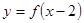 的图象关于
的图象关于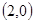 成中心对称,若
成中心对称,若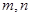 满足不等式
满足不等式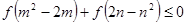 .则当
.则当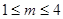 时,
时,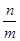 的取值范围是( )
的取值范围是( )