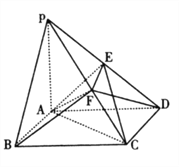
题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于M,抛物线C的焦点为F,且
交于M,抛物线C的焦点为F,且![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设点Q是抛物线C上的动点,点D,E在y轴上,圆![]() 内切于三角形
内切于三角形![]() ,求三角形
,求三角形![]() 的面积的最小值.
的面积的最小值.
【答案】(Ⅰ)![]() (Ⅱ)8
(Ⅱ)8
【解析】
(Ⅰ)根据抛物线的定义得到点![]() 的坐标,将其代入抛物线方程即可得到结果;
的坐标,将其代入抛物线方程即可得到结果;
(Ⅱ)设![]() ,
,![]() ,
,![]() 且
且![]() ,利用直线
,利用直线![]() 与圆
与圆![]() 相切可得
相切可得![]() ,同理可得
,同理可得![]() ,所以
,所以![]() ,
,![]() 是方程
是方程![]() 的两根.利用根与系数的关系求出
的两根.利用根与系数的关系求出![]() ,再根据三角形面积公式与基本不等式可得答案.
,再根据三角形面积公式与基本不等式可得答案.
(Ⅰ)因为直线![]() 与抛物线
与抛物线![]() 交于M,且
交于M,且![]() .
.
根据抛物线的定义可知,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,因为
,因为![]() ,所以解得
,所以解得![]() ,
,
∴抛物线方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() 且
且![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由直线![]() 与圆
与圆![]() 相切,
相切,
得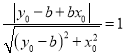 ,注意到
,注意到![]() ,
,
化简得![]() ,
,
同理得![]()
所以![]() ,
,![]() 是方程
是方程![]() 的两根,
的两根,
所以![]() ,
,![]() ,
,
所以![]()
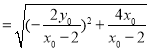
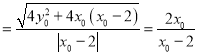 ,
,
∴![]() (当且仅当
(当且仅当![]() 时等号成立)
时等号成立)
因此三角形![]() 的面积的最小值为8.
的面积的最小值为8.

【题目】过去五年,我国的扶贫工作进入了“精准扶贫”阶段.目前“精准扶贫”覆盖了全部贫困人口,东部帮西部,全国一盘棋的扶贫格局逐渐形成.到2020年底全国830个贫困县都将脱贫摘帽,最后4335万贫困人口将全部脱贫,这将超过全球其他国家过去30年脱贫人口总和.2020年是我国打赢脱贫攻坚战收官之年,越是到关键时刻,更应该强调“精准”.为落实“精准扶贫”政策,某扶贫小组,为一“对点帮扶”农户引种了一种新的经济农作物,并指导该农户于2020年初开始种植.已知该经济农作物每年每亩的种植成本为1000元,根据前期各方面调查发现,该经济农作物的市场价格和亩产量均具有随机性,且两者互不影响,其具体情况如下表:
该经济农作物亩产量(kg) |
|
| 该经济农作物市场价格(元/kg) |
|
| |
概率 |
|
| 概率 |
|
|
(1)设2020年该农户种植该经济农作物一亩的纯收入为X元,求X的分布列;
(2)若该农户从2020年开始,连续三年种植该经济农作物,假设三年内各方面条件基本不变,求这三年中该农户种植该经济农作物一亩至少有两年的纯收入不少于16000元的概率;
(3)2020年全国脱贫标准约为人均纯收入4000元.假设该农户是一个四口之家,且该农户在2020年的家庭所有支出与其他收入正好相抵,能否凭这一亩经济农作物的纯收入,预测该农户在2020年底可以脱贫?并说明理由.