题目内容
(本小题满分12分)已知直线 经过直线
经过直线 与
与 的交点.
的交点.
(1)若点 到
到 的距离为3,求
的距离为3,求 的方程;
的方程;
(2)求点 到
到 的距离的最大值,并求此时
的距离的最大值,并求此时 的方程.
的方程.
 经过直线
经过直线 与
与 的交点.
的交点.(1)若点
 到
到 的距离为3,求
的距离为3,求 的方程;
的方程;(2)求点
 到
到 的距离的最大值,并求此时
的距离的最大值,并求此时 的方程.
的方程.(1)直线l的方程为
(2) ,
, .
.

(2)
 ,
, .
.解:(1)解:联立 得交点P (2,1).设l的方程为
得交点P (2,1).设l的方程为
(k存在),即
 ,得
,得 ,
,
即 .
.
当k不存在时,直线 ,此时点A(5,0)到l的距离也为3.
,此时点A(5,0)到l的距离也为3.
 直线l的方程为
直线l的方程为 …………(6分)
…………(6分)
(2)由 解得交点P(2,1),如图,过P任作一直线l,设d为定点A到l的距离,则
解得交点P(2,1),如图,过P任作一直线l,设d为定点A到l的距离,则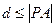 (当
(当 时等号成立).
时等号成立). 


 即:
即: .………(12分)
.………(12分)
 得交点P (2,1).设l的方程为
得交点P (2,1).设l的方程为
(k存在),即

 ,得
,得 ,
,即
 .
.当k不存在时,直线
 ,此时点A(5,0)到l的距离也为3.
,此时点A(5,0)到l的距离也为3. 直线l的方程为
直线l的方程为 …………(6分)
…………(6分)(2)由
 解得交点P(2,1),如图,过P任作一直线l,设d为定点A到l的距离,则
解得交点P(2,1),如图,过P任作一直线l,设d为定点A到l的距离,则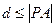 (当
(当 时等号成立).
时等号成立). 


 即:
即: .………(12分)
.………(12分)
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
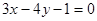 的距离为2的直线方程为 ( )
的距离为2的直线方程为 ( )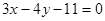 B.
B.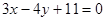
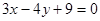 D
D  与直线
与直线 互相垂直,则
互相垂直,则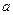 的值是 ( )
的值是 ( )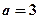 ”是“直线
”是“直线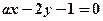 ”与“直线
”与“直线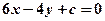 平行”的 ( )
平行”的 ( )
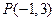 且垂直于直线
且垂直于直线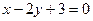 的直线方程为 .
的直线方程为 . 及圆
及圆 ,则过点
,则过点 ,且在圆上截得的弦为最长的弦所在的直线方程是
,且在圆上截得的弦为最长的弦所在的直线方程是



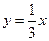 绕原点顺时针旋转
绕原点顺时针旋转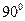 ,再向左平移1个单位,所得到的直线的方程为( )
,再向左平移1个单位,所得到的直线的方程为( ) 



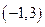 且平行于直线
且平行于直线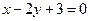 的直线方程为 。
的直线方程为 。