题目内容
已知函数y=
，x∈[1，2]对于满足1＜x1＜x2＜2的任意x1，x2，给出下列结论：
①f（x2）-f（x1）＞x2-x1
②x2f（x1）＞x1f（x2）；
③（x2-x1）[f（x2）-f（x1）]＜0
④（x1-x2）[f（x2）-f（x1）]＞0
其中正确结论的个数有（ ）
| 1-(x-1)2 |
①f（x2）-f（x1）＞x2-x1
②x2f（x1）＞x1f（x2）；
③（x2-x1）[f（x2）-f（x1）]＜0
④（x1-x2）[f（x2）-f（x1）]＞0
其中正确结论的个数有（ ）
分析：将函数表达式，化简得（x-1）2+y2=1，其中x∈[1，2]，y≥0．作出它的图象，得到以（1，0）为圆心，半径为1的圆的上半圆的右半部分．再根据直线的斜率公式与函数的单调性，分别对各项中的结论加以验证，可得②③为真命题而①④为假命题，即可得到本题答案．
解答：解：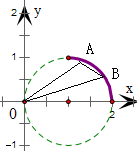
令y=
，化简得（x-1）2+y2=1，其中x∈[1，2]，y≥0
得函数的图象为以（1，0）为圆心，半径为1的圆的上半圆的右半部分，如图所示
对于①，f（x2）-f（x1）＞x2-x1等价于
＞1
观察图象，可得在图象上任意取两点A（x1，f（x1）），B（x2，f（x2））
线段AB的斜率为负数，故不等式
＞1不成立，得①不正确；
对于②，注意到x2、x1都是正数，
不等式x2f（x1）＞x1f（x2）等价于
＞
，
结合1＜x1＜x2＜2，可得A、B两点与原点的连线斜率满足kOA＞kOB，②正确
对于③，由于函数y=
在x∈[1，2]上为减函数，可得当x2＜x1时，f（x2）＞f（x1）．
因此（x2-x1）[f（x2）-f（x1）]＜0，可得③正确；
对于④，由于结论与③矛盾，故④不正确
综上所述，正确的命题为②③
故选：B
令y=| 1-(x-1)2 |
得函数的图象为以（1，0）为圆心，半径为1的圆的上半圆的右半部分，如图所示
对于①，f（x2）-f（x1）＞x2-x1等价于
| f(x2)-f(x1) |
| x2-x1 |
观察图象，可得在图象上任意取两点A（x1，f（x1）），B（x2，f（x2））
线段AB的斜率为负数，故不等式
| f(x2)-f(x1) |
| x2-x1 |
对于②，注意到x2、x1都是正数，
不等式x2f（x1）＞x1f（x2）等价于
| f(x1) |
| x1 |
| f(x2) |
| x2 |
结合1＜x1＜x2＜2，可得A、B两点与原点的连线斜率满足kOA＞kOB，②正确
对于③，由于函数y=
| 1-(x-1)2 |
因此（x2-x1）[f（x2）-f（x1）]＜0，可得③正确；
对于④，由于结论与③矛盾，故④不正确
综上所述，正确的命题为②③
故选：B
点评：本题给出特殊函数，判断几个结论正确与否，着重考查了函数的单调性与图象的作法、直线的斜率公式等知识，属于中档题．
练习册系列答案
相关题目