题目内容

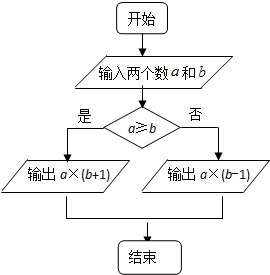定义某种运算s=a?b，运算原理如图所示，则式子：(2tan
5π
4
)?lne+lg100?(
1
3
)-1的值是（　　）
分析：先根据流程图中即要分析出计算的类型，该题是考查了分段函数，再求出函数的解析式，然后根据解析式求解函数值即可．
解答：解：该算法是一个分段函数y=
a×(b+1)a≥b
a×(b-1)a＜b

∵(2tan
5π
4
)=2，lne=1，lg100=2，(
1
3
)-1=3
∴原式=2?1+2?3=2×（1+1）+2×（3-1）=8．
故选B．
点评：本题主要考查了选择结构，根据流程图计算运行结果是算法这一模块的重要题型，属于基础题．
练习册系列答案
相关题目
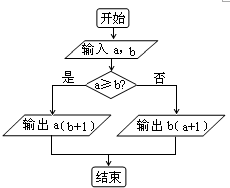精英家教网定义某种运算S=a?b，运算原理如图所示，则式子(2tan
5π
4
)?lne+(lg100)?(
1
3
)-1的值为（　　）
A、13B、11C、8D、4
定义某种运算S=a?b，运算原理如框图所示，则式子2?lne+2?(
1
3
)-1的值为（　　）精英家教网
A、13B、11C、8D、4
定义某种运算S=a?b，运算原理如图所示，则式子：（2tan
5π
4
）?lne+lg100?(
1
27
)-
1
3
的值是
4
4
．
（2013•青岛一模）定义某种运算S=a?b，运算原理如框图所示，则式子(2tan
π
4
)?lne+lg100?(
1
3
)-1的值为
13
13
．
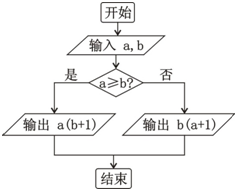精英家教网如图，定义某种运算S=a?b，运算原理如图所示，则式子（2tan
5π
4
）?lne+1g100?（
1
3
）-1的值为（　　）
A、11B、13C、8D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网