题目内容
7. 若函数f(x)和g(x)的定义域、值域都是R,则不等式f(x)> g(x)有解的充要条件是 ( )
| A.$ x∈R, f(x)>g(x) | B.有无穷多个x (x∈R ),使得f(x)>g(x) |
| C." x∈R,f(x)>g(x) | D.{ x∈R| f(x)≤g(x)}=F |
A
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
、函数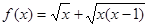 的定义域为 ( )
的定义域为 ( )
A.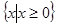 | B.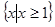  | C.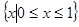 | D.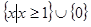 |
已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
| A.(0,1) | B.(1,2) |
| C.(0,2) | D.[2,+∞) |
已知函数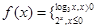 ,则
,则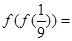 ( )
( )
| A.4 | B.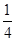 | C.-4 | D.-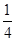 |
已知函数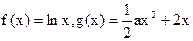 ,若
,若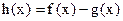 存在单调减区间,则实数
存在单调减区间,则实数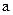 的取值范围是( )
的取值范围是( )
A.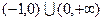 | B.(0,1) | C.(-1,0) | D.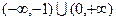 |
函数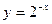 的值域是( )
的值域是( )
| A.R | B.(-∞,0) | C.(-∞,1) | D.(0,+∞) |
定义在R上的函数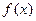 的反函数为
的反函数为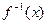 ,且对任意的x都有
,且对任意的x都有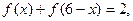 若ab=
若ab= 100,则
100,则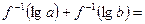 ( )
( )
| A.2 | B.3 | C.4 | D.6 |
已知函数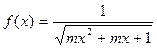 的定义域是
的定义域是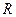 ,则实数
,则实数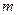 的取值范围是( )
的取值范围是( )
A.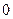 < <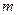 < <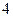 | B.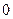 ≤ ≤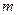 ≤ ≤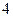 | C.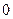 ≤ ≤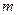 < <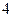  | D. ≥ ≥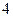 |