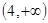题目内容
已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
| A.(0,1) | B.(1,2) |
| C.(0,2) | D.[2,+∞) |
B
解析

练习册系列答案
相关题目
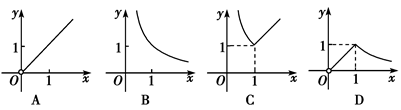
若函数f(x)=在(0,+∞)上为增函数,则a的取值范围是( )
| A.(-∞,0) | B.(0,+∞) |
| C.R | D.[-1,1] |
设函数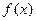 和g(x
和g(x )分别是R上的偶函数和奇函数,则下列结论恒成立的是
)分别是R上的偶函数和奇函数,则下列结论恒成立的是
A.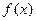 +|g(x)|是偶函数 +|g(x)|是偶函数 | B.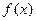 -|g(x)|是奇函数 -|g(x)|是奇函数 |
C.|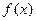 | +g(x)是偶函数 | +g(x)是偶函数 | D.|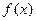 |- g(x)是奇函数 |- g(x)是奇函数 |
f(x),g(x)是定义在R上的函数,h(x)=f(x)+g(x),则“f(x),g(x)均为偶函数”是“h(x)为偶函数”的( )
| A.充要条件 |
| B.充分而不必要的条件 |
| C.必要而不充分的条件 |
| D.既不充分也不必要的条件 |
设集合A和集合B都是实数集R,映射f:A→B是把集合A中的元素x对应到集合B中的元素x3-x+1,则在映射f下象1的原象所组成的集合是
( )
| A.{1} | B.{0} |
| C.{0,-1,1} | D.{0,1,2} |
设函数f(x)是定义在R上周期为3的奇函数,若f(1)<1,f(2)=,则
| A.a<-1或a>0 | B.-1<a<0 |
| C.a<且a≠-1 | D.-1<a<2 |
7. 若函数f(x)和g(x)的定义域、值域都是R,则不等式f(x)> g(x)有解的充要条件是 ( )
| A.$ x∈R, f(x)>g(x) | B.有无穷多个x (x∈R ),使得f(x)>g(x) |
| C." x∈R,f(x)>g(x) | D.{ x∈R| f(x)≤g(x)}=F |
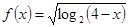 的定义域为( )
的定义域为( )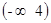 B.
B.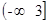 C.
C.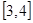 D.
D.