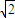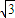题目内容
正四棱锥的底面边长等于2
，侧面与底面成60°的二面角，此四棱锥体积为（ ）
| 3 |
| A、9 | B、12 | C、15 | D、18 |
分析：画出正四棱锥图形，根据题意，侧面与底面成60°的二面角，求出棱锥的高，即可求出体积．
解答：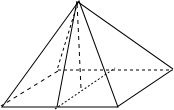
解：由题意作出图形如图：
因为侧面与底面成60°的二面角，
所以棱锥的高为：
tan60°=3，
所以棱锥的体积：
×2
×2
×3=12．
故选B．
解：由题意作出图形如图：因为侧面与底面成60°的二面角，
所以棱锥的高为：
| 3 |
所以棱锥的体积：
| 1 |
| 3 |
| 3 |
| 3 |
故选B．
点评：本题考查棱柱、棱锥、棱台的体积，棱锥的结构特征，二面角及其度量，还考查计算能力，是基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
正四棱锥的底面边长为2，侧棱长为
，其主视图和侧视图是全等的等腰三角形，则正视图的周长为（ ）
| 3 |
A、2+2
| ||
B、3+
| ||
C、2+
| ||
D、2+2
|
，其主视图和侧视图是全等的等腰三角形，则正视图的周长为
，其主视图和侧视图是全等的等腰三角形，则正视图的周长为（ ）
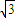
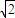
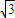，其主视图和侧视图是全等的等腰三角形，则正视图的周长为（ ）
