题目内容
以下四个命题中,真命题的个数是( )
①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;
②若p∨q为假命题,则p、q均为假命题;
③命题p:存在x∈R,使得x2+x+1<0,则-p:任意x∈R,都有x2+x+1≥0
④在△ABC中,A<B是sinA<sinB的充分不必要条件.
①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;
②若p∨q为假命题,则p、q均为假命题;
③命题p:存在x∈R,使得x2+x+1<0,则-p:任意x∈R,都有x2+x+1≥0
④在△ABC中,A<B是sinA<sinB的充分不必要条件.
分析:根据逆否命题的定义,可得①是真命题;根据含有逻辑词“或”的命题真假的判断,可得②是真命题;根据含有量词的命题否定方法,可得③是真命题;根据正弦定理和充要条件的判断,可得④是假命题.由此可得答案.
解答:解:对于①,命题“若p则q”的逆否命题是“若非q则非p”
故命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,可得①正确;
对于②,命题“p∨q”只要存在真命题它就是真命题
而p∨q为假命题,说明p、q中没有真命题,得它们均为假命题,可得②正确;
对于③,含有量词的命题“存在x∈R,p(x)”的否定是“任意x∈R,-p(x)”
故命题p“存在x∈R,使得x2+x+1<0”的否定-p是“任意x∈R,都有x2+x+1≥0”,可得③正确;
对于④,在△ABC中,A<B等价于a<b,根据正弦定理得到sinA<sinB
故在△ABC中,A<B是sinA<sinB的充要条件,可得④不正确
综上所述,真命题是①②③,共3个
故选:C
故命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,可得①正确;
对于②,命题“p∨q”只要存在真命题它就是真命题
而p∨q为假命题,说明p、q中没有真命题,得它们均为假命题,可得②正确;
对于③,含有量词的命题“存在x∈R,p(x)”的否定是“任意x∈R,-p(x)”
故命题p“存在x∈R,使得x2+x+1<0”的否定-p是“任意x∈R,都有x2+x+1≥0”,可得③正确;
对于④,在△ABC中,A<B等价于a<b,根据正弦定理得到sinA<sinB
故在△ABC中,A<B是sinA<sinB的充要条件,可得④不正确
综上所述,真命题是①②③,共3个
故选:C
点评:本题给出几个命题,要求我们找出其中的真命题的个数.着重考查了逆否命题定义、逻辑联结词、含有题词的命题的否定和正弦定理等知识,属于中档题.

练习册系列答案
相关题目
已知-
<θ<
,且sinθ+cosθ=a,其中a∈(0,1),则关于tanθ的值,在以下四个答案中,可能正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、-3 | ||
B、3或
| ||
C、-
| ||
D、-3或-
|
 ,且
,且 其中
其中 ,则关于
,则关于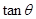 的值,在以下四个答案中,可能正确的是 (
)
的值,在以下四个答案中,可能正确的是 (
) B.3 或
B.3 或 C.
C. D.
D.


