题目内容
14、已知各顶点都在同一球面上的正四棱锥高为3,体积为6,则这个球的表面积是
16π
.分析:画出图形,正四棱锥P-ABCD的外接球的球心在它的高PO1上,记为O,求出PO1,OO1,解出球的半径,求出球的表面积;正四棱锥P-ABCD的五个顶点在同一球面上,若该正四棱锥的底面边长为4,侧棱长为 $2\sqrt{6}$,进而可得答案.
解答: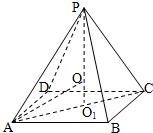 解:正四棱锥P-ABCD的外接球的球心在它的高PO1上,
解:正四棱锥P-ABCD的外接球的球心在它的高PO1上,
记为O,PO=AO=R,PO1=3,OO1=4-R,
在Rt△AO1O中,R2=3+(3-R)2得R=2,
∴球的表面积S=16π
故答案为:16π
 解:正四棱锥P-ABCD的外接球的球心在它的高PO1上,
解:正四棱锥P-ABCD的外接球的球心在它的高PO1上,记为O,PO=AO=R,PO1=3,OO1=4-R,
在Rt△AO1O中,R2=3+(3-R)2得R=2,
∴球的表面积S=16π
故答案为:16π
点评:本题考查球的表面积,球的内接体问题,解答关键是利用直角三角形列方程式求解球的半径,是基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目