题目内容
如图，在等腰三角形ABC中，底边BC=2，| AD |
| DC |
| AE |
| 1 |
| 2 |
| EB |
| BD |
| AC |
| 1 |
| 2 |
| CE |
| BD |
-
| 2 |
| 3 |
-
．| 2 |
| 3 |
分析：可取BC的中点O作为坐标建立坐标系．利用向量的坐标运算，求出两向量的坐标，即可得出答案．
解答：解：∵在等腰三角形ABC中，底边BC=2，
∴可取BC的中点O作为坐标原点建立如图所示的坐标系．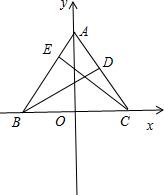
∴B（-1，0），C（1，0），设A（0，a）（a＞0），
∵
=
，∴D为AC的中点，∴D（
，
），
∴
=（
，
），
=（1，-a），
∵
•
=-
，∴
-
a2=-
，解得a=2
∴A（0，2），又∵
=
，∴
=
，
∴
=
+
=（0，2）+
（-1，-2）=（-
，
）
∴
=（-
，
）-（1，0）=（-
，
）
∴
•
=（-
，
）•（
，1）=-
故答案为：-
∴可取BC的中点O作为坐标原点建立如图所示的坐标系．
∴B（-1，0），C（1，0），设A（0，a）（a＞0），
∵
| AD |
| DC |
| 1 |
| 2 |
| a |
| 2 |
∴
| BD |
| 3 |
| 2 |
| a |
| 2 |
| AC |
∵
| BD |
| AC |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴A（0，2），又∵
| AE |
| 1 |
| 2 |
| EB |
| AE |
| 1 |
| 3 |
| AB |
∴
| OE |
| OA |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
∴
| CE |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
∴
| CE |
| BD |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
故答案为：-
| 2 |
| 3 |
点评：本题考查数量积的运算，建立平面直角坐标系是解决问题的关键，属中档题．
练习册系列答案
相关题目
如图，在等腰直角三角形ABC中，则AM＜AC的概率为（ ）
（2013•徐州一模）如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且
．
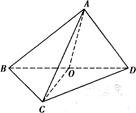
时，求证：AO⊥平面BCD；
的大小为
时，求二面角
的正切值．
如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且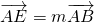
，
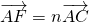，其中m，n∈（0，1）．若EF，BC的中点分别为M，N，且m+4n=1，则
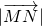的最小值为________．
如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且
，
，其中m，n∈（0，1）．若EF，BC的中点分别为M，N，且m+4n=1，则
的最小值为 ．