题目内容
移动公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为| 1 | 5 |
(1)求ξ的分布列;
(2)试说明小李出资50元增加1张奖券是否划算.
分析:(1)由题意知ξ的所有可能取值为2450,1450,450,-550,结合变量对应的事件和独立重复试验的概率公式,写出变量的概率,得到随机变量的分布列.
(2)根据上一问的分布列做出期望值,设出小李出资50元增加1张奖券消费的实际支出为ξ1(元),写出变量的分布列,做出期望值,两个期望值进行比较,得到小王出资50元增加1张奖券划算.
(2)根据上一问的分布列做出期望值,设出小李出资50元增加1张奖券消费的实际支出为ξ1(元),写出变量的分布列,做出期望值,两个期望值进行比较,得到小王出资50元增加1张奖券划算.
解答:解:(1)由题意知ξ的所有可能取值为2450,1450,450,-550,
P(ξ=2450)=(
)3=
P(ξ=1450)=C31(
)×(
)3=
p(ξ=450)=C32(
×(
)=
p(ξ=-550)=C33(
)3=
,
∴ξ分布列为
(2)由上一问知道
Eξ=2450×
+1450×
+450×
+(-550)×
=1850(元)
设小李出资50元增加1张奖券消费的实际支出为ξ1(元)
则P(ξ1=2400)=(
)2=
P(ξ1=1400)=
P(ξ1=400)=
(
)2=
∴Eξ1=2400×
+1400×
+400×
=2000
∴Eξ<Eξ1
故小王出资50元增加1张奖券划算.
P(ξ=2450)=(
| 4 |
| 5 |
| 64 |
| 125 |
P(ξ=1450)=C31(
| 1 |
| 5 |
| 4 |
| 5 |
| 48 |
| 125 |
p(ξ=450)=C32(
| 1 |
| 5 |
| 4 |
| 5 |
| 12 |
| 125 |
p(ξ=-550)=C33(
| 1 |
| 5 |
| 1 |
| 125 |
∴ξ分布列为
| ξ | 2450 | 1450 | 450 | -550 | ||||||||
| P |
|
|
|
|
Eξ=2450×
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
设小李出资50元增加1张奖券消费的实际支出为ξ1(元)
则P(ξ1=2400)=(
| 4 |
| 5 |
| 16 |
| 25 |
P(ξ1=1400)=
| 48 |
| 125 |
P(ξ1=400)=
| C | 2 2 |
| 1 |
| 5 |
| 1 |
| 25 |
∴Eξ1=2400×
| 16 |
| 25 |
| 48 |
| 125 |
| 1 |
| 25 |
∴Eξ<Eξ1
故小王出资50元增加1张奖券划算.
点评:本题考查离散型随机变量的分布列,考查离散型随机变量的期望,本题是一个实际问题,题目的情景比较好,可以引起同学们的兴趣.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为
,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为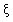 (元);
(元); 的分布列;
的分布列;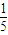 ,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为ξ(元);
,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为ξ(元);